Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М., 1980. 6 страница
Тогда
Задача 1.2. Решить однородную систему линейных алгебраических уравнений
С помощью элементарных преобразований матрицу
Следовательно,
Откуда
Полагая
Задача 1.3. По координатам точек а). Модуль вектора
б). Скалярное произведение векторов
в). Проекцию вектора
г). Координаты точки
Задача 1.4. Даны векторы
а). Найти модуль векторного произведения
б). Проверить, будут ли коллинеарны или ортогональны два вектора
Условие коллинеарности двух векторов Т.к. Условие ортогональности двух векторов
Т.к.
в). Вычислить смешанное произведение трех векторов
г). Проверить, будут ли компланарны три вектора Вектора Из пункта в)
Задача 1.5. Даны четыре точки Составить уравнения: а). Плоскости Уравнение плоскости по трем точкам имеет вид
б). Прямой Уравнение прямой по двум точкам
в). Прямой Из уравнения плоскости
г). Прямой
д). Плоскости, проходящей через точку Вектор Значит,
е). Вычислить
ж). Косинус угла между координатной плоскостью Вектор
Задача 1.6. Составить уравнение плоскости, проходящей через точки
Найти вектор
Тогда уравнение искомой плоскости
Задача 1.7. Найти уравнение прямой, проходящей через точку пересечения прямых
Вектор
Задача 1.8. Определить вид поверхности и построить ее.
а)
Получим уравнение однополостного гиперболоида, ось которого совпадает с
X
б) Приведем уравнение к каноническому виду Это уравнение конуса второго порядка, ось которого совпадает с осью 0Z.
X
4.2. Решение типового варианта контрольной работы N 2
Задача 2.1. Найти Решение. а). Для
б). Для
в). Для
Задача 2.2. Найти
Решение а).
б). Дифференцируя уравнение для
откуда
Дифференцирование последнего соотношения дает
Внося выражение для
в). Первая производная заданной параметрически функции вычисляется по формуле
Здесь
откуда
Вторую производную вычислим по формуле
Задача 2.3. Вычислить предел, пользуясь правилом Лопиталя:
Решение. а). Искомый предел является неопределённостью типа По правилу Лопиталя
б). Предел является неопределённостью вида
К последнему (типа
Полученный предел вновь является неопределенностью
в). Предел является неопределенностью вида
Тогда
Вычислим вспомогательный предел
Искомый предел согласно (1) равен
Задача 2.4. Исследовать функцию Решение. Областью определения является вся действительная ось
Тогда Для отыскания участков выпуклости используется вторая производная
При Вертикальных асимптот функция не имеет. Для отыскания наклонных асимптот
Поэтому при Результаты исследования с учетом четности функции
|





 приведем к трапециевидной форме
приведем к трапециевидной форме ~
~  .
. 2<3 и система имеет бесконечное множество решений, зависящих от 3-2=1 произвольной постоянной. Исходная система эквивалентна
2<3 и система имеет бесконечное множество решений, зависящих от 3-2=1 произвольной постоянной. Исходная система эквивалентна

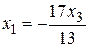 .
. (произвольной постоянной), имеем
(произвольной постоянной), имеем ,
, 
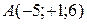 ,
,  ,
,  найти:
найти:


 ;
; .
. и
и  .
. .
. на вектор
на вектор  .
. .
. , делящей отрезок
, делящей отрезок  в отношении 1:3;
в отношении 1:3;  . Следовательно:
. Следовательно:


 Необходимо:
Необходимо: .
.
 ;
; .
. .
.
 то вектора
то вектора 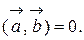
 то вектора неортогональны.
то вектора неортогональны.

 .
. .
. компланарны, если
компланарны, если 
 следовательно, эти векторы некомпланарны.
следовательно, эти векторы некомпланарны.

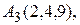


 , откуда
, откуда  .
.
 откуда
откуда 
 , перпендикулярной к плоскости
, перпендикулярной к плоскости  .
. ||
|| 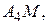 откуда уравнение
откуда уравнение 
 , параллельной
, параллельной  и уравнение этой прямой имеет вид
и уравнение этой прямой имеет вид 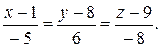
 перпендикулярно к прямой
перпендикулярно к прямой 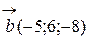 перпендикулярен искомой плоскости.
перпендикулярен искомой плоскости. - ее уравнение, которое приводится к виду
- ее уравнение, которое приводится к виду 
 - угла между прямой
- угла между прямой  и плоскостью
и плоскостью  ;
; 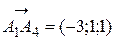 ;
;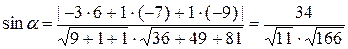 .
. и плоскостью
и плоскостью  а вектор
а вектор  . Поэтому
. Поэтому .
. и
и  параллельно прямой, проведенной через точки
параллельно прямой, проведенной через точки  и
и 
 , перпендикулярный искомой плоскости. Вектор
, перпендикулярный искомой плоскости. Вектор  и
и 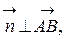 следовательно, в качестве вектора
следовательно, в качестве вектора 
 ;
;  ;
;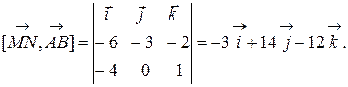
 которое приводится к виду
которое приводится к виду 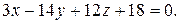
 и
и  перпендикулярно первой прямой. Найдем точку
перпендикулярно первой прямой. Найдем точку  :
:
 параллелен искомой прямой. Поэтому ее уравнение запишем как
параллелен искомой прямой. Поэтому ее уравнение запишем как 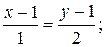 оно приводится к виду
оно приводится к виду 
 . Приведем уравнение к каноническому виду
. Приведем уравнение к каноническому виду
 полуоси эллипса в плоскости Y0Z равны
полуоси эллипса в плоскости Y0Z равны  и
и  Построим поверхность.
Построим поверхность. Z
Z





 Y
Y

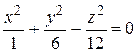 .
. Z
Z







 Y
Y


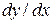 , если
, если  ,
,  ,
,  .
. имеем
имеем
 .
.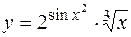 .
.
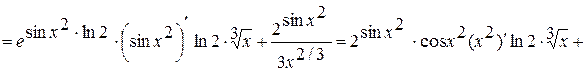
 .
. .
.


 .
.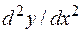 , если
, если



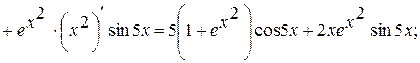



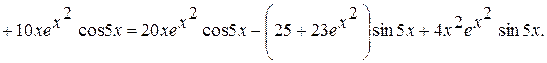
 , имеем
, имеем
 ,
,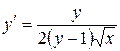 .
.
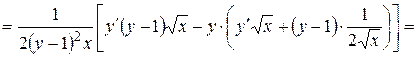
 .
. , находим
, находим .
. .
.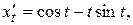
 ,
, .
.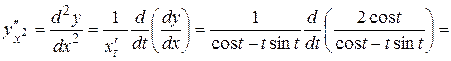
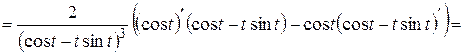


 .
.

 .
.

 .
. поэтому вначале его надо преобразовать к виду
поэтому вначале его надо преобразовать к виду  или
или 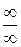 :
: .
. ) можно применять правило Лопиталя:
) можно применять правило Лопиталя: .
. поэтому повторное применение правила дает
поэтому повторное применение правила дает .
. к которой удобно применять следующий прием. Обозначим
к которой удобно применять следующий прием. Обозначим
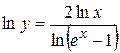 .
. . (1)
. (1)
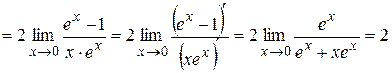 .
. .
. и построить ее график.
и построить ее график. . Для отыскания участков монотонности находим
. Для отыскания участков монотонности находим .
. при
при  (интервал возрастания),
(интервал возрастания),  при
при  (интервал убывания). Точка
(интервал убывания). Точка  является стационарной, поскольку
является стационарной, поскольку 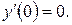 При переходе через
При переходе через  .
. или
или  будет
будет 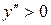 и функция вогнута; при
и функция вогнута; при 
 и функция выпукла.
и функция выпукла.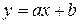 вычислим
вычислим
 .
. функция имеет асимптоту
функция имеет асимптоту 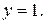
 показаны на графике
показаны на графике Y
Y 



 2
2


 1
1



