Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М., 1980. 8 страница
Сведем двойной интеграл к повторному интегралу
Задача 4.9. Вычислить с помощью тройного интеграла объем области V, ограниченной указанными поверхностями: V: y=8-2x2, z=0, y=0, x=0, z=2x+y.
Решение. Область V изображена на рисунке, где цифрами 1, 2 обозначены параболический цилиндр y=8-2x2 и плоскость z=2x+y соответственно; остальные уравнения отвечают координатным плоскостям.
y
0 C
Объем
Приведем интеграл к повторному
Через
Задача 4.10. Вычислить: а) заряд проводника, располагающегося вдоль кривой
Решение. а). Заряд q проводника, имеющего плотность заряда
(1). Окружность удобно задать в параметрическом виде:
Участку L соответствуют значения параметра
откуда
причем верхний знак выбирается при В данной задаче
(2). Для дуги параболы L удобнее использовать частный случай формулы при
Для
Используем подстановку
Тогда
б). Работа силового поля с компонентами
(1). Для четверти окружности приведем интеграл к определенному по формуле
(2). Для дуги параболы
Задача 4.11. Вычислить расход жидкости с полем скоростей
Решение. Искомый расход дан формулой
Единичная нормаль к плоскости имеет компоненты
Поверхностный интеграл можно выразить через двойной интеграл
где уравнение поверхности
Область
Внося в двойной интеграл заданные функции, находим
Последний запишется через повторный интеграл
С о д е р ж а н и е
Учебное издание
Высшая математика
Программа, методические указания и контрольные задания для студентов-заочников инженерных и инженерно-экономических специальностей приборостроительного факультета
В 2-х частях
Ч а с т ь I
Составители: ИБРАГИМОВ Владислав Ахмедович СТРЕЛЬЦОВ Сергей Викторович МЕЛЕШКО Алексей Николаевич ВИШНЕВСКАЯ Ольга Геннадьевна
Редактор Т.Н.Микулик
Формат 60х84 1/16. Бумага тип. № 2. Офсет. печать. Усл.печ.л. 5,9. Уч.-изд.л. 4,5. Тираж 200. Заказ 544.
Белорусская государственная политехническая академия. Лицензия ЛВ № 155 от 30.01.98. 220027, Минск, пр. Ф.Скорины, 65.
Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М., 1980. 2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисления. - М.: Наука, 1980. 3. Бугров Я.С., Никольский С.М. Дифференциальные уравнения, кратные интегралы, ряды, функции комплексного переменного. - М.: Наука, 1981. 4. Ефимов А.В. Краткий курс аналитической геометрии. - М.: Наука, 1965. 5. Герасимович А.И. Математическая статистика. – Мн., 1983. 6. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высш. школа, 1972. 7. Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика. - М.: Высш. школа, 1982. 8. Элементы линейной алгебры / Под ред. Р.Ф.Апатенок. - Мн.: Выш. школа, 1977. 9. Араманович В.Г., Левин В.И. Уравнения математической физики. - М.: Наука, 1964. 10. Сборник индивидуальных заданий по высшей математике. В 3 ч. / Под ред. проф. А.П.Рябушко. – Мн.: Выш. школа, 1990. 11. Сборник индивидуальных заданий по теории вероятностей и математической статистике / Под ред. проф. А.П.Рябушко. – Мн.: Выш. школа, 1992.
Дополнительная литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисления. В 2 т. - М.: Высш. школа, 1981. 2. Воеводин В.В. Линейная алгебра. - М.: Физматгиз, 1980. 3. Жевняк Р.М., Карпук А.А. Высшая математика. В 5 ч. – Мн.: Выш. школа, 1985.
2.2. Программа курса «Высшая математика» для экономических специальностей
Тема 1. Элементы линейной алгебры и аналитической геометрии Матрицы, определители. Операции над матрицами. Обратная матрица. Системы линейных уравнений и неравенств и их геометрический смысл. Экономическая интерпретация многомерных векторов и матриц и их использование в плановых расчетах.
|

 .
.









 8 - B
8 - B
 V 2
V 2

 1 4 -
1 4 - D
D S
S



 области посредством тройного интеграла запишется
области посредством тройного интеграла запишется
 .
. обозначены аппликаты точек
обозначены аппликаты точек  (см. рис.), вычисленные из уравнений плоскости
(см. рис.), вычисленные из уравнений плоскости  и плоскости
и плоскости  , т.е.
, т.е.  ,
,  . Через
. Через  обозначена область плоскости
обозначена область плоскости  , на которую проецируется область
, на которую проецируется область  . Поэтому при сведении двойного интеграла по области
. Поэтому при сведении двойного интеграла по области  точек
точек  вычисляются из уравнения
вычисляются из уравнения  и уравнения линии, являющейся пересечением цилиндрической поверхности
и уравнения линии, являющейся пересечением цилиндрической поверхности  и плоскости
и плоскости  т.е. уравнения
т.е. уравнения  Искомый объем равен
Искомый объем равен



 , с плотностью
, с плотностью  с помощью криволинейного интеграла первого рода; b) работу силы
с помощью криволинейного интеграла первого рода; b) работу силы  вдоль траектории L от т. A до т. B с помощью криволинейного интеграла второго рода.
вдоль траектории L от т. A до т. B с помощью криволинейного интеграла второго рода. - четверть окружности
- четверть окружности 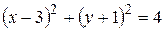 между А(3,-3), В(5,-1). (2)
между А(3,-3), В(5,-1). (2)  - дуга параболы
- дуга параболы  от А (0,1) до В (1,-1).
от А (0,1) до В (1,-1). .
. .
. где
где

 Криволинейный интеграл выражается через определенный
Криволинейный интеграл выражается через определенный
 и нижний - при
и нижний - при 



 имеем
имеем


 вдоль траектории АВ запишется
вдоль траектории АВ запишется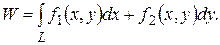




 , протекающей за единицу времени через часть
, протекающей за единицу времени через часть  лежащей в первом октанте. Единичная нормаль
лежащей в первом октанте. Единичная нормаль  направлена вне начала координат.
направлена вне начала координат.

 .
. .
. ,
,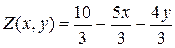 .
. является проекцией
является проекцией  .
. .
.
 Подписано в печать 21.01.2000.
Подписано в печать 21.01.2000.


