Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М., 1980. 1 страница
При несоблюдении указанных требований работа не рецензируется. Прорецензированные и зачтенные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления зачтенных контрольных работ студент не допускается к сдаче зачета и экзамена.
3.2. Выбор варианта контрольной работы
Номер варианта для каждой задачи выбирается по двум последним цифрам номера зачетной книжки. Если это число превышает 30, то из него вычитается число, кратное 30, так, чтобы остаток оказался меньше 30. Этот остаток есть номер варианта. Например, номер зачетной книжки оканчивается на 76. Тогда номер варианта задания равен
76-2*30=16.
Примечание. Количество и содержание заданий контрольных работ, выполняемых в каждом семестре, определяется студентам на установочной сессии.
3.3. Задания контрольных работ
К о н т р о л ь н а я р а б о т а № 1
Линейная алгебра и аналитическая геометрия
Задание 1.1
Проверить совместность системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса.
Задание 1.2
Решить однородную систему линейных алгебраических уравнений.
Задание 1.3
По координатам точек a, b и с для указанных векторов найти: а) модуль вектора а; б) скалярное произведение векторов a и в) проекцию вектора c на вектор d; г) координаты точки M, делящей отрезок l в отношении 1. A (4, 6, 3), B (-5, 2, 6), C (4, -4, -3), a =
2. A (4, 3, -2), B (-3, -1, 4), C (2, 2, 1), a =
3. A (-2, -2, 4), B (1, 3, -2), C (1, 4, 2), a = 4. A (2, 4, 3), B (3, 1, -4), C (-1, 2, 2), a =
5. A (2, 4, 5), B (1, -2, 3), C (-1, -2, 4), a =
6. A (-1, -2, 4), B (-1, 3, 5), C (1, 4, 2), a =
7. A (1, 3, 2), B (2, 4, 1), C (1, 3, 2), a =
8. A (2, -4, 3), B (-3, -2, 4), C (0, 0, -2), a =
9. A (3, 4, -4), B (-2, 1, 2), C (2, -3, 1), a =
10. A (0, 2, 5), B (2, -3, 4), C (3, 2, -5), a =
11. A (-2,-3, -4), B (2, -4, 0), C (1, 4, 5), a =
12. A (-2, -3, -2), B (1, 4, 2), C (1, -3, 3), a =
13. A (5, 6, 1), B (-2, 4,-1), C (3,-3,3), a =
14. A (10, 6, 3), B (-2, 4, 5), C (3, -4, -6), a = 15. A (3, 2, 4), B (-2, 1, 3), C (2, -2, -1), a =
16. A (-2, 3, -4), B (3, -1, 2), C (4, 2, 4), a =
17. A (4, 5, 3), B (-4, 2, 3), C (5, -6, -2), a =
18. A (2, 4, 6), B (-3, 5, 1), C (4, -5, -4), a =
19. A (-4, -2, -5), B (3, 7, 2), C (4, 6, -3), a =
20. A (5, 4, 4), B (-5, 2, 3), C (4, 2, -5), a =
21. A (3, 4, 6), B (-4, 6, 4), C (5, -2, -3), a =
22. A (-5, -2, -6), B (3, 4, 5), C (2, -5, 4), a =
23. A (3, 4, 1), B (5, -2, 6), C (4, 2, -7), a = 24. A (4, 3, 2), B (-4, -3, 5), C (6, 4, -3), a =
25. A (-5, 4, 3), B (4, 5, 2), C (2, 7, -4), a = 26. A (6, 4, 5), B (-7, 1, 8), C (2, -2, -7), a =
27. A (6, 5, -4), B (-5, -2, 2), C (3, -3, 2), a =
28. A (-3, -5, 6), B (3, 5, -4), C (2, 6, 4), a =
29. A (3, 5, 4), B (4, 2, -3), C (-2, 4, 7), a =
30. A (4, 6, 7), B (2, -4, 1), C (-3, -4, 2), a =
Задание 1.4
Даны векторы
|


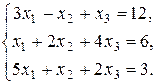

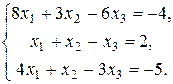
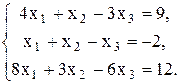


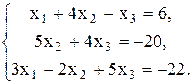



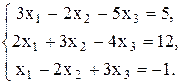





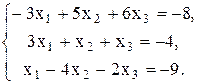


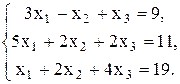








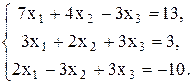
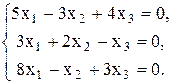














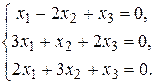








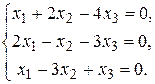





 b;
b; .
.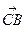 -
-  , b =
, b =  , c =
, c =  = 5,
= 5,  = 4.
= 4. , b =
, b =  , b =
, b =  , c =
, c = 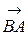 +
+  , b =
, b =  , c = b, d =
, c = b, d = 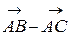 , b =
, b =  = 2,
= 2,  , c = b =
, c = b =  , d =
, d =  , B =
, B =  -
-  , b = c =
, b = c =  -
-  , d =
, d =  , l = AB,
, l = AB,  = 5.
= 5. +
+  = 3,
= 3,  , b = c =
, b = c =  = 2.
= 2.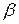 = 2.
= 2. +
+  , b = c =
, b = c =  , d =
, d =  = 1,
= 1,  , d =
, d =  , l = BA,
, l = BA, 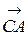 , b =
, b =  -
-  . Необходимо: а) найти модуль векторного произведения векторов
. Необходимо: а) найти модуль векторного произведения векторов 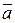 и
и  ; б) проверить, будут ли коллинеарны или ортогональны два вектора
; б) проверить, будут ли коллинеарны или ортогональны два вектора  и
и  ; в) вычислить смешанное произведение трех векторов
; в) вычислить смешанное произведение трех векторов  и проверить, будут ли они компланарны.
и проверить, будут ли они компланарны.


