Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М., 1980. 5 страница
Задача 4.9.
Вычислить с помощью тройного интеграла объем области
Задача 4.10.
Вычислить: (а) заряд проводника, располагающегося вдоль кривой (b) работу силы
между
Задача 4.11.
С помощью поверхностного интеграла первого рода
вычислить расход
4. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КОНТРОЛЬНЫХ РАБОТ
4.1. Решение типового варианта контрольной работы №1
Задача 1.1. Дана система линейных неоднородных алгебраических уравнений
Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований расширенную матрицу
Следовательно,
а). По формулам Крамера:
Находим
б). С помощью обратной матрицы
Решение системы
т.е.
в). Наша система эквивалентна
(прямой ход Гаусса совершен при нахождении рангов матриц
|

 , ограниченной указанными поверхностями.
, ограниченной указанными поверхностями.



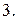

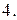

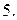
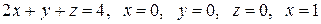
















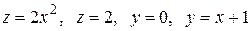


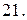

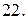



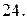

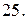
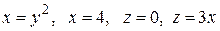
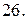

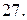

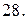

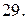


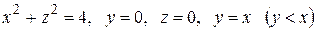
 с плотностью
с плотностью  с помощью криволинейного интеграла первого рода
с помощью криволинейного интеграла первого рода 
 вдоль траектории
вдоль траектории  до точки
до точки  с помощью криволинейного интеграла второго рода
с помощью криволинейного интеграла второго рода 
 - отрезок прямой между
- отрезок прямой между 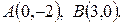
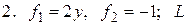 - дуга параболы
- дуга параболы  между
между 
 - отрезок прямой между
- отрезок прямой между 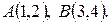
 - четверть окружности
- четверть окружности  между
между 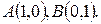
 - дуга параболы
- дуга параболы  между
между 
 - дуга параболы
- дуга параболы  между
между 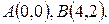
 - отрезок прямой между
- отрезок прямой между 
 - четверть окружности
- четверть окружности  между
между
 - дуга параболы
- дуга параболы  между
между 
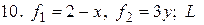 - полуокружность
- полуокружность  между
между
 - дуга параболы
- дуга параболы 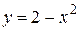 между
между 

 - полуокружность
- полуокружность 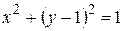 между
между 




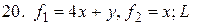 - дуга параболы
- дуга параболы  между
между 
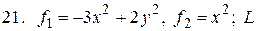 - отрезок прямой между
- отрезок прямой между 
 - полуокружность
- полуокружность 


 - полуокружность
- полуокружность 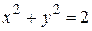 между
между






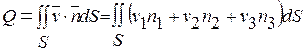
 жидкости с полем скоростей
жидкости с полем скоростей протекающей за единицу времени через часть
протекающей за единицу времени через часть 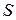 плоскости
плоскости  лежащую в первом октанте. Единичная нормаль
лежащую в первом октанте. Единичная нормаль 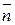 направлена вне начала координат.
направлена вне начала координат.






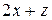


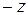

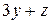








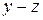












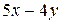







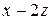
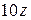







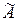 приведем к трапециевидной форме
приведем к трапециевидной форме


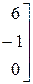 ~
~ 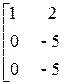

 ~
~ 

 .
. (числу неизвестных системы). Значит, исходная система совместна и имеет единственное решение.
(числу неизвестных системы). Значит, исходная система совместна и имеет единственное решение.

 где
где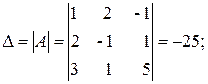

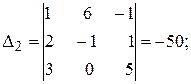
 .
.

 .
. где
где  - обратная матрица к
- обратная матрица к  ,
,  - столбец правых частей.
- столбец правых частей. .
. ;
;  ;
;  ;
; ;
;  ;
; 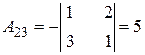 ;
; ;
;  ;
;  .
. ,
,
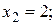
 .
.



