Задание 41
3а) Как определяется число степеней свободы статистики Стьюдента при оценке значимости оцененных коэффициентов? 3б) Почему невозможно составить таблицы критических значений статистики Дарбина-Уотсона? 3в) Что из следующего не относится к признакам мультиколлинеарности: а) некоторые коэффициенты модели незначимы, б) ранг матрицы в) частный коэффициент корреляции для двух регрессоров близок к единице, г) коэффициент корреляции для двух объясняющих переменных равен 0.9. 3г) Найдите оценки b1 и b2 коэффициентов уравнения регрессии y = β1x1 + β2x2 + ε; по трем наблюдениям:
Задание 42
3а) Если оцененный коэффициент значим на 5-процентном уровне, будет ли он значим на 1-процентом уровне? 3б) Какое предположение обеспечивает возможность устранения автокорреляции при помощи авторегрессионного преобразования? 3) Модель множественной регрессии содержит а) множество выборочных данных, б) много зависимых переменных, в) несколько объясняющих переменных, г) не менее одного регрессора.
3г) Проверьте гипотезу об отсутствии гетероскедастичности в модели y = β1 + β2x + β3z + ε по методу Голдфелда-Квандта, если сумма квадратов остатков в регрессии по первым 7 наблюдениям равна 1.58, а по последним 7 наблюдениям - равна 9.36. Всего наблюдений 34. В таблице приведены критические значения распределения Фишера для 5-процентного уровня значимости:
|

 равен
равен 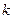 ,
,


