УРАВНЕНИЕ КАСАТЕЛЬНОЙ
ПРИМЕР Напишите уравнения всех касательных к графику функции y = x3 – 3x2 + 3, параллельных прямой y = 9x + 1. Решение. 1. a – абсцисса точки касания.
4. 1) a = – 1; y = 9x + 8 – уравнение касательной; 1) a = 3; y = 9x – 24 – уравнение касательной.
Семестр: 1 Разработал преподаватель: Барсукова Е.В.. Перед тем как приступить к решению задач контрольной работы нужно изучить соответствующий теоретический материал. Этот материал нужно закрепить, решая самостоятельно задачи, соответствующие рассматриваемому теоретическому материалу. После этого приступайте к решению задачи контрольной работы, одновременно сверяясь с уже решенной аналогичной типовой задачей, разобранной во время аудиторных занятий. Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от номера варианта каждого студента (номер варианта соответствует номеру в списке группы по журналу). Для того, чтобы получить свои личные данные, необходимо выбрать из таблиц параметры k, l, m и n, соответствующие своему варианту. Эти числа нужно подставить в условия задач контрольной работы.
Задание 1 Даны три вектора
Найти 1. 2.скалярное произведение векторов 3.косинус угла между векторами
Задание 2 Дана матрица А= Найти 1. AT 2. определитель матрицы А 3. A+ mAT 4. AAT
Задание 3 Решить систему уравнений Ax=y, где A= 1. методом Крамера 2. методом Гаусса 3. методом обратной матрицы Задание 4 Найдите пределы функций.
Задание 5 Найдите производные
Задание 5. Составить уравнения касательных к графику функции параллельных прямой
|

 Но, с другой стороны, f '(a) = 9 (условие параллельности). Значит, надо решить уравнение 3a2 – 6a = 9. Его корни a = – 1, a = 3 (рис. 3).
Но, с другой стороны, f '(a) = 9 (условие параллельности). Значит, надо решить уравнение 3a2 – 6a = 9. Его корни a = – 1, a = 3 (рис. 3). =(k,l, m, n);
=(k,l, m, n); =(l, n, -k, -m);
=(l, n, -k, -m); =(m, k, -n, -l);
=(m, k, -n, -l); = n
= n  +m
+m  -n
-n 
 ;
; 
 , x=
, x= 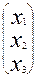 , y=
, y= 


 функций
функций







