Решение. Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицы
Чтобы матрицу Пример:
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно. Следует отметить, что в ряде случаев можно умножать матрицы и так, и так. Как умножить матрицы? Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей. Начнем с самого простого: Пример: Умножить матрицу
Пример сложнее: Умножить матрицу Формула:
В результате получена так называемая нулевая матрица. Попробуйте самостоятельно выполнить умножение Умножьте матрицу Вот готовое решение.
апишем систему трех алгебраических уравнений в удобном для решения виде
Найдем детерминант системы по правилу треугольников
Для вычисления дополнительных определителей подставляем столбец свободных членов на место первого, второго и третьего столбцов. В результате получим
Вычисляем неизвестные за формулами Крамера
Для данного примера нахождения решения также не слишком сложно, хотя по сравнению с системой двух уравнений вычислений заметно прибавилось.
На первом этапе нужно записать расширенную матрицу системы: Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями. Существуют следующие элементарные преобразования: 1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули. 4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу 5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера: На практике так подробно, конечно, не расписывают, а пишут короче: «Переписываю матрицу и переписываю первую строку: «Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: «Теперь второй столбец. Вверху –1 умножаю на –2: «И третий столбец. Вверху –5 умножаю на –2: Вернемся к нашей системе Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке. (2) Делим вторую строку на 3. Цель элементарных преобразований – привести матрицу к ступенчатому виду: В результате элементарных преобразований получена эквивалентная исходной система уравнений: Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса. В нижнем уравнении у нас уже готовый результат: Рассмотрим первое уравнение системы Ответ: Решить методом Гаусса систему уравнений: Запишем расширенную матрицу системы: Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: Сначала смотрим на левое верхнее число: Теперь первая строка у нас останется неизменной до конца решения. Уже легче. Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах: Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2: Результат записываем во вторую строку: Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3: Результат записываем в третью строку: На практике эти действия обычно выполняются устно и записываются в один шаг: Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО: Далее нужно получить единицу на следующей «ступеньке»: В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение: На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь: Для этого к третьей строке прибавляем вторую строку, умноженную на –2: Последнее выполненное действие – причёска результата, делим третью строку на 3. В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: В третьем уравнении у нас уже готовый результат: Смотрим на второе уравнение: И, наконец, первое уравнение: Ответ: Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока). Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений. Пример 11 Решить систему с матричным методом Решение: Запишем систему в матричной форме: Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице Решение системы найдем по формуле Согласно формуле нам нужно найти обратную матрицу Обратную матрицу найдем по формуле: Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке. Внимание! Если Теперь нужно вычислить 9 миноров и записать их в матрицу миноров Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент: В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать
Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее). Таким образом:
Повторюсь, выполненные шаги мы подробно разбирали на уроке Как найти обратную матрицу? Теперь записываем обратную матрицу:
Ни в коем случае не вносим Осталось провести матричное умножение. Умножать матрицы можно научиться на уроке Действия с матрицами. Кстати, там разобран точно такой же пример.
Обратите внимание, что деление на 60 выполняется в последнюю очередь. Ответ:
пример
Любой предел состоит из трех частей: 1) Всем известного значка предела Сама запись Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»? Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Готово. Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию. Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко! Пример с бесконечностью:
Разбираемся, что такое А что в это время происходит с функцией Итак: если
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию Еще один пример с бесконечностью:
Опять начинаем увеличивать Вывод: при И еще серия примеров: Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет. Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: Что нужно запомнить и понять из вышесказанного?
|


 можно было умножить на матрицу
можно было умножить на матрицу  нужно, чтобы число столбцов матрицы
нужно, чтобы число столбцов матрицы на матрицу
на матрицу  ?
?
 , значит, умножать данные матрицы можно.
, значит, умножать данные матрицы можно.
 , следовательно, выполнить умножение невозможно:
, следовательно, выполнить умножение невозможно:
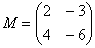 и
и  возможно как умножение
возможно как умножение  , так и умножение
, так и умножение 
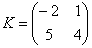 на матрицу
на матрицу  – попытайтесь сразу уловить закономерность.
– попытайтесь сразу уловить закономерность.


 ).
). на матрицу
на матрицу 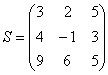









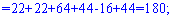








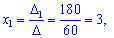

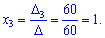
 и решим ее методом Гаусса.
и решим ее методом Гаусса. . По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления. . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:
. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: 
 . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:
. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:  . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
. Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы. , и ко второй строке прибавляем первую строку умноженную на –2:
, и ко второй строке прибавляем первую строку умноженную на –2:  . Теперь первую строку можно разделить «обратно» на –2:
. Теперь первую строку можно разделить «обратно» на –2:  . Как видите, строка, которую ПРИБАВЛЯ ЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯ ЮТ.
. Как видите, строка, которую ПРИБАВЛЯ ЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯ ЮТ.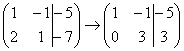
 »
» , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку:
, и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку:  »
» . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку:
. Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку:  »
» . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку:
. Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: 
 . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.
. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.
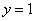 .
.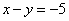 и подставим в него уже известное значение «игрек»:
и подставим в него уже известное значение «игрек»:



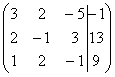

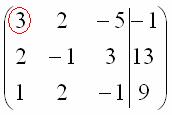









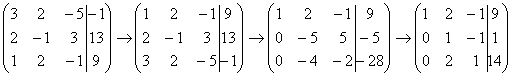
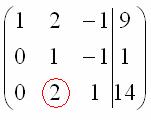



 . Значение «зет» уже известно, таким образом:
. Значение «зет» уже известно, таким образом:

 . «Игрек» и «зет» известны, дело за малым:
. «Игрек» и «зет» известны, дело за малым:




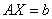 , где
, где 
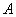 нужно было бы поставить нули.
нужно было бы поставить нули. (её подробный вывод можно посмотреть в статье Матричные уравнения).
(её подробный вывод можно посмотреть в статье Матричные уравнения). и выполнить матричное умножение
и выполнить матричное умножение  . Алгоритм нахождения обратной матрицы подробно разобран на уроке Как найти обратную матрицу?
. Алгоритм нахождения обратной матрицы подробно разобран на уроке Как найти обратную матрицу? , где
, где  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 
 , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса).
, то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса).

 находится в первой строке, третьем столбце, а, например, элемент
находится в первой строке, третьем столбце, а, например, элемент  находится в 3 строке, 2 столбце
находится в 3 строке, 2 столбце


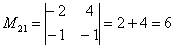




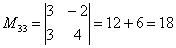
 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы  – матрица алгебраических дополнений.
– матрица алгебраических дополнений. – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
 в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.


 .
.  . Запись читается «икс стремится к единице». Чаще всего – именно
. Запись читается «икс стремится к единице». Чаще всего – именно  , хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (
, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ( ).
). .
. , затем
, затем  ,
,  , …,
, …,  , ….
, …. 

 ? Это тот случай, когда
? Это тот случай, когда  , потом
, потом  , потом
, потом  , затем
, затем  и так далее до бесконечности.
и так далее до бесконечности. ?
?  ,
,  ,
,  , …
, …
 бесконечность и получаем ответ.
бесконечность и получаем ответ.

 неограниченно возрастает:
неограниченно возрастает:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
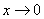 , то
, то  ,
,  ,
,  .
. , то все равно
, то все равно  , так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
, так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.


