Когда дан любой предел, сначала просто пытаемся подставить число в функцию.2) Вы должны понимать и сразу решать простейшие пределы, такие как Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с очень интересными случаями, когда предела функции вообще не существует! На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов.
Пределы с неопределенностью вида Сейчас мы рассмотрим группу пределов, когда Пример: Вычислить предел Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида Как решать пределы данного типа? Сначала мы смотрим на числитель и находим Теперь смотрим на знаменатель и тоже находим Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке. Итак, метод решения следующий: для того, чтобы раскрыть неопределенность
Вот оно как, ответ Что принципиально важно в оформлении решения? Во-первых, указываем неопределенность, если она есть. Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо? Пример 2 Найти предел
Разделим числитель и знаменатель на
Пример 3 Найти предел
Разделим числитель и знаменатель на
Под записью Таким образом, при раскрытии неопределенности вида
Пределы с неопределенностью вида Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать МАТЕМАТИЧЕСКИЙ АНАЛИЗ Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу. Пример 4 Решить предел Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше. Итак, решаем наш предел Разложим числитель и знаменатель на множители Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение: В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе. ! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка. Далее находим корни: Таким образом: Всё. Числитель на множители разложен. Знаменатель. Знаменатель
Очевидно, что можно сократить на
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим числитель на множители.
Пример 5 Вычислить предел Сначала «чистовой» вариант решения
Разложим числитель и знаменатель на множители. Числитель:
Что важного в данном примере? Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем. Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус. ! Важно Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.
|
, 
, 
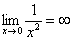и т.д.
и метод их решения
, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
в старшей степени:
, а вовсе не бесконечность.
, он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.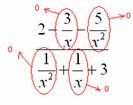
делим числитель и знаменатель на 
.
)
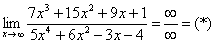
. Чистовой вариант решения может выглядеть так:
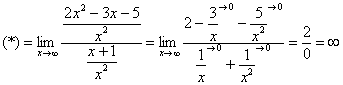
подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
и метод их решения
предлагаю читать далее.
.
.
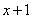уже является простейшим множителем, и упростить его никак нельзя.
:
, 
встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки). 
, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.
