ПОСТОЯННЫЙ ТОК. где dq – количество заряда, прошедшего через поперечное сечение проводника за время dt.
6.1. Сила тока:
где dq – количество заряда, прошедшего через поперечное сечение проводника за время dt. Если ток постоянный:
где q – заряд, прошедший через поперечное сечение за время t. 6.2. Плотность тока:
6.3. Закон Ома: · для однородного участка цепи (рис.11):
· для неоднородного участка цепи (рис.12):
· где R, r – соответственно внешнее и внутреннее сопротивления. 6.4. Законы Кирхгофа.
где n – число токов, сходящихся в узле.
где n – число участков, содержащих активное сопротивление;
При решении задач по законам Кирхгофа необходимо: 1. Обозначить на схеме узлы и контуры. 2. Произвольно выбрать направление токов (если они не оговорены условием задачи) во всех участках цепи и обозначить их на чертеже стрелками. 3. Учесть направление токов при составлении первого закона (положительными считаются токи, входящие в узел, а отрицательными – выходящие из узла). 4. Составить систему уравнений для первого закона Кирхгофа. Число уравнений, составленных по этому закону, должно быть на единицу меньше числа узлов в цепи. 5. Выбрать произвольно направление обхода контуров. Считать, что ЭДС в уравнении будет положительной, если направление от отрицательного полюса источника тока к положительному совпадает с направлением обхода, в противном случае ЭДС следует считать отрицательной (рис.15). 6. Считать падение напряжения в цепи (IR) положительным, если выбранное ранее направление тока на этом участке (между двумя узлами) совпадает с направлением обхода контура, и отрицательным, если направление тока не совпадает с направлением обхода контура. 7. Первый контур выбрать произвольно. При составлении уравнений для следующих контуров надо включать в них контуры, не входившие в предыдущие уравнения. 8. Число уравнений, составленных по второму закону Кирхгофа, определяется, исходя из условия, что если число контуров в цепи равно m, а число узлов в ней n, то число независимых уравнений, достаточных для решения, будет равно 9. Получение в ответе токов с отрицательными знаками означает, что было выбрано направление, обратное действительному.
6.5. Сопротивление проводника длиной l, площадью поперечного сечения S и удельным сопротивлением ρэ:
· при последовательном соединении (Рис.16а)
· при параллельном соединении (Рис.16б)
где R i – сопротивление отдельного i проводника.
6.7. Работа тока при напряжении U и силе тока I за время t:
6.8. Мощность тока:
6.9. Закон Джоуля – Ленца:
где Q – количество теплоты, выделившейся в проводнике при прохождении по нему тока I за время t.
Примеры решения задач.
Пример 7. Между двумя вертикальными пластинами, находящимися на расстоянии Δх=1см друг от друга, на нити висит заряженный шарик, масса которого равна 0,1 г. После того как на пластины была подана разность потенциалов 1000 В, нить с шариком отклонилась на угол 100. Найти заряд шарика.
Дано: Найти: q. Решение. Пусть для определенности q > 0. На шарик действуют сила тяжести Сила, с которой электрическое поле действует на заряд, помещенный в это поле:
где Электрическое поле конденсатора является однородным, поэтому
где Шарик находится в равновесии, следовательно
В проекциях на координатные оси «x»и «y» получим систему уравнений: x: y: откуда следует, что Приравнивая выражения для силы получим: откуда
Выполним вычисления:
Ответ: q = 1,7
Пример 8. Электрическое поле образовано положительно заряженной бесконечно длинной нитью. Двигаясь под действием этого поля от точки, находящейся на расстоянии х1 = 1 см от нити, до точки х2 = 4 см,
Дано: х1 = Найти: τ; Решение. Электрическое поле совершает работу по перемещению, α; – частицы, изменяя тем самым кинетическую энергию
где W2, W1 – кинетические энергии α; – частицы в точках поля с потенциалами Работа по перемещению заряда в электрическом поле: А12=q (φ1-φ2) (2) где (φ1-φ2) – разность потенциалов между точками поля (рис.18). Разность потенциалов найдем, используя связь между напряженностью и разностью потенциалов для неоднородного поля:
где Подставим выражение для разности потенциалов (3) в формулу работы (2):
Приравняв выражения работы (1) и (4), получим:
Проверим размерность:
Выполним вычисления:
Пример 9. На рисунке 19 приведена схема электрической цепи батареи с e = 120 В; R3 = 20 Ом; R4 = 25 Ом, падение потенциала на сопротивлении R1 равно U1 = 40 В. Амперметр показывает ток 2 А. Найти сопротивление R2. Сопротивлением батареи и амперметра пренебречь.
Дано: e = 120 В; R3 = 20 Ом; R4 = 25 Ом; U1 = 40 В; IA = 2 А. Найти: R2. Решение. Сопротивления IA = I2 + I3, (1)
где IA, I2, I3 – соответственно общий ток, токи в нагрузках R2 и R3; По закону Ома для участка цепи:
отсюда
ЭДС источника равна сумме падений напряжений на всех участках цепи:
откуда
В (4) падение напряжения на сопротивлении R4 заменим соотношением В результате получим:
Используя (2) рассчитаем ток через сопротивление R3: I3 = Учитывая (1) рассчитаем ток через сопротивление R2: I2 = IA – I3 = 2 – 1,5 = 0,5 А. Определим
Ответ: R2 = 60 Ом
Дано: Найти: Решение. Силы токов в разветвленной цепи определим с помощью правил Кирхгофа. Для этого составим столько уравнений, чтобы их число было равно числу искомых величин. Перед составлением уравнений выберем произвольно направления токов на всех участках цепи и направления обхода контуров (рис. 20) Воспользуемся первым правилом Кирхгофа, учитывая, что ток, входящий в узел, входит в уравнение со знаком “+”, а ток, выходящий из узла – со знаком “–”. Для узла А
или
При составлении уравнений по второму правилу Кирхгофа учтём, что если направление тока на участке контура совпадает с выбранным направлением обхода, то соответствующее произведение если при обходе контура внутри источника тока осуществляется переход от “–” к “+”, то соответствующая Для контуров: 1) ACDBА:
2) CDFEС:
Подставив значения
Решим эту систему с помощью определителей. Для этого запишем её в виде:
Искомые токи найдем по формулам:
Найдем определители
Тогда
Знак “минус” у тока Ответ: Пример 11. Сила тока в проводнике сопротивлением Дано: Найти: Решение. Согласно закону Джоуля-Ленца для бесконечно малого промежутка времени:
По условию задачи сила тока равномерно растет, т.е.
Тогда можно записать:
Проинтегрировав (1) и подставив выражение для
Выполним вычисления:
Ответ:
|

 ,
, .
. ,
, где
где  - ток, прошедший через площадь поперечного сечения
- ток, прошедший через площадь поперечного сечения  , перпендикулярного направлению движения зарядов.
, перпендикулярного направлению движения зарядов.
 ;
; ;
; для замкнутого контура (рис.13):
для замкнутого контура (рис.13):  ,
, - разность потенциалов на концах участка;
- разность потенциалов на концах участка; 6.4.1. Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю; т. е.
6.4.1. Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю; т. е. ,
, 6.4.2. Второй закон Кирхгофа: в любом замкнутом контуре разветвленной цепи алгебраическая сумма произведений сил токов Ii на сопротивление Ri соответствующих участков этого контура равна алгебраической сумме ЭДС
6.4.2. Второй закон Кирхгофа: в любом замкнутом контуре разветвленной цепи алгебраическая сумма произведений сил токов Ii на сопротивление Ri соответствующих участков этого контура равна алгебраической сумме ЭДС  , встречающихся в этом контуре; т. е.
, встречающихся в этом контуре; т. е.
 – число источников в контуре.
– число источников в контуре. .
. .
. 6.6. Сопротивление проводников:
6.6. Сопротивление проводников:
 ;
; ,
, .
. .
. ,
,
 м; m =
м; m =  кг;
кг;  В;
В;  .
. , сила натяжения нити
, сила натяжения нити  и сила кулоновского взаимодействия
и сила кулоновского взаимодействия  (рис.17).
(рис.17). (1)
(1) - напряженность поля, образованного двумя пластинами (поле плоского конденсатора) однородно,
- напряженность поля, образованного двумя пластинами (поле плоского конденсатора) однородно,  .
. , (2)
, (2) - разность потенциалов между пластинами;
- разность потенциалов между пластинами;  - расстояние между ними.
- расстояние между ними. .
. или
или  ;
; или
или  ,
, . (3)
. (3) (1) и (3), учитывая (2),
(1) и (3), учитывая (2), ,
, .
. нКл.
нКл. Кл.
Кл. - частица изменила свою скорость от
- частица изменила свою скорость от  1= 2
1= 2  м/с до
м/с до  м/с. Найти линейную плотность заряда на нити τ;.
м/с. Найти линейную плотность заряда на нити τ;.
 м; х2 = 4
м; х2 = 4  м;
м;  м/с;
м/с; 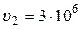 м/с.
м/с. (1)
(1) и
и  , (3)
, (3) - напряженность поля, созданного заряженной нитью в точке на расстоянии х от нити
- напряженность поля, созданного заряженной нитью в точке на расстоянии х от нити  ;
;  - линейная плотность заряда нити.
- линейная плотность заряда нити. . (4).
. (4). .
.
 Кл/м.
Кл/м. Ответ:
Ответ:  .
. и
и 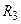 соединены параллельно (Рис19), следовательно:
соединены параллельно (Рис19), следовательно: , (2)
, (2) - падения напряжения на сопротивлениях
- падения напряжения на сопротивлениях  и
и  .
. ,
,  ,
, . (3)
. (3) ,
, . (4)
. (4)
 В.
В. А.
А. Ом
Ом Пример 10. Три источника тока с ЭДС
Пример 10. Три источника тока с ЭДС  В,
В,  В,
В,  В и внутренними сопротивлениями
В и внутренними сопротивлениями  Ом и три реостата с сопротивлениями
Ом и три реостата с сопротивлениями  Ом,
Ом,  Ом,
Ом,  Ом соединены, как показано на рисунке 20. Определить силу тока в реостатах.
Ом соединены, как показано на рисунке 20. Определить силу тока в реостатах.
 ,
,
 входит в уравнение со знаком “плюс”, в противном случае – со знаком “минус”;
входит в уравнение со знаком “плюс”, в противном случае – со знаком “минус”; входит в уравнение со знаком “плюс”, в противном случае – со знаком “минус”.
входит в уравнение со знаком “плюс”, в противном случае – со знаком “минус”. ; (1)
; (1) . (2)
. (2) в соотношения (1) и (2), получим систему уравнений:
в соотношения (1) и (2), получим систему уравнений: .
.
 ;
;  ;
; 
 :
:



 А;
А;  А;
А;  А.
А. говорит о том, что направление тока на рисун-
говорит о том, что направление тока на рисун- ;
;  ;
;  .
. равномерно растет от
равномерно растет от  до
до  за время
за время  . Определить выделившееся в проводнике за это время количество теплоты.
. Определить выделившееся в проводнике за это время количество теплоты. ,
,  ,
,  .
. .
. , где
, где 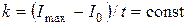 .
. (1)
(1) .
. .
. .
.


