Примеры решения задач. Пример 1. Точка движется вдоль оси Х так, что координата х с течением времени изменяется согласно уравнению х=A+Bt+Ct2
Пример 1. Точка движется вдоль оси Х так, что координата х с течением времени изменяется согласно уравнению х = A+Bt+Ct2, где А= 3 м, В =2 м/с, С =1 м/с2. Найти среднюю скорость тела за первую и вторую секунды движения.
Дано: х =A+Bt+Ct2; А =3 м; В =2 м/с; С =1 м/с2. Найти: Решение. По определению средняя скорость тела – это отношение пути, пройденного телом за время D t, к величине этого промежутка времени:
Выясним, меняет ли точка направление движения в данные интервалы времени. Для этого найдем проекцию мгновенной скорости на ось х:
Получили, что во все моменты времени Путь, пройденный телом за первую секунду:
где В нашем случае t0 =0 c, t1 =1с, следовательно, путь ΔS1:
Средняя скорость за первую секунду:
Аналогично путь, пройденный телом за вторую секунду:
Средняя скорость за вторую секунду:
Ответ: 3 м/с, 5 м/с.
Пример 2. Небольшое тело брошено со скоростью υ0 = 10м/с под углом 450 к горизонту. Найти радиус кривизны траектории тела через 1с после начала движения. Сопротивление воздуха не учитывать. Дано: Найти: R.
Рис.4 Рис.5 Движение тела происходит в поле силы тяжести, роль полного ускорения выполняет ускорение, сообщаемое телу силой тяжести, т.е.
Сопротивление воздуха отсутствует, поэтому проекция вектора скорости
Проекция скорости
В верхней точке траектории
Так как t1<t, следовательно, тело прошло высшую точку траектории и находится на спуске, например в точке А (рис.4, 5). Полное ускорение тела в точке А равно ускорению свободного падения В тоже время:
Приравняв соотношения (3) и (4), получим:
Следовательно, для нахождения радиуса кривизны траектории необходимо найти скорость тела в момент времени t. Модуль скорости
определяемые по формулам (1) и (2):
Вычислим скорость
Ответ:
Пример 3. Пуля, летящая горизонтально, попадает в шар, подвешенный на очень легком жестком стержне, и застревает в нем. Масса пули mn в тысячу раз меньше массы шара mш. Расстояние от точки подвеса стержня до центра шара равно 1 м. Найти скорость пули при условии, что стержень с пулей отклонился от вертикального положения от удара пули на угол 100.
Найти: Решение. Пусть в момент удара шар находился в положении D. В результате взаимодействия с пулей шар поднялся на некоторую высоту h = СD. Полагая шар материальной точкой, можно записать на основании закона сохранения импульса для неупругого удара:
где По закону сохранения механической энергии для системы «шар - пуля»:
Из рис.6 следует:
откуда Так как Преобразуем соотношения (1) и (2), учтя, что
Из уравнений (3)и (5) находим скорость шара с пулей, полученную в момент удара пули:
Проверим размерность:
Выполним вычисления:
Ответ:
Пример 4. Найти кинетическую энергию платформы, движущейся со скоростью 9 км/ч, если масса платформы вместе с колесами 78 кг. Колеса считать однородными дисками. Общая масса колес 3 кг.
Дано: mп = 78 кг; 4 mк =m=3 кг; Найти: Ек. Решение. Кинетическая энергия платформы складывается из энергии поступательного движения Епост платформы как целого и кинетической энергии вращательного движения четырех колес Евр:
где I – момент инерции колеса (сплошного диска) массой mk и радиуса r относительно оси вращения, проходящей через центр колеса ( Учитывая, что
Поэтому полная кинетическая энергия платформы
Ответ: 250 Дж.
|

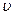 ср1,
ср1,  .
. .
. , направление движения точки не меняется.
, направление движения точки не меняется. ,
, и
и  - координаты точки в моменты времени
- координаты точки в моменты времени 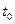 и
и  .
. м
м м/с.
м/с. м.
м. м/с.
м/с. = 10 м/с;
= 10 м/с;  ; t = 1 с.
; t = 1 с. Решение: Будем рассматривать движение тела в прямоугольной системе координат xoy, считая тело материальной точкой.
Решение: Будем рассматривать движение тела в прямоугольной системе координат xoy, считая тело материальной точкой.
 .
. на ось ox постоянна:
на ось ox постоянна: . (1)
. (1) . (2)
. (2) , поэтому в момент времени t1, когда тело достигает высшей точки траектории:
, поэтому в момент времени t1, когда тело достигает высшей точки траектории: ,
, с.
с. , направлено вертикально вниз и перпендикулярно проекции скорости
, направлено вертикально вниз и перпендикулярно проекции скорости  . Нормальное ускорение
. Нормальное ускорение  перпендикулярно вектору скорости
перпендикулярно вектору скорости  следует:
следует: или
или  . (3)
. (3) . (4)
. (4) . (5)
. (5)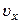 ,
, 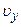 :
: , (6)
, (6) . (7)
. (7) м/с.
м/с. м.
м. м.
м. Дано:
Дано:  ;
; 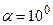 ; l = 1 м.
; l = 1 м. .
.
 , (1)
, (1) . (2)
. (2) ,
, . (3)
. (3)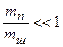 , то
, то  .
. , получим:
, получим: ; (4)
; (4) . (5)
. (5) .
. .
. м/с.
м/с. = 9 км/ч=2,5 м/c.
= 9 км/ч=2,5 м/c. ,
, ,
, 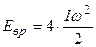 ;
; ).
). ,
,  , а
, а  , получим:
, получим: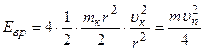 .
. Дж.
Дж.


