ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
2.1. Основное уравнение динамики (второй закон Ньютона):
где 2.2. В классической физике при
2.3. Закон сохранения импульса для изолированной системы:
где N – число материальных точек (тел), входящих в систему. 2.4. Теорема о движении центра масс: Центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы, под действием результирующей внешних сил:
2.5. Работа силы. · Элементарная работа силы
· Полная работа силы на всем пути S:
где ·
где модуль вектора перемещения равен пройденному пути (
2.6. Мощность силы. Рис.2 · Средняя мощность за интервал времени
· Мгновенная мощность:
2.7. Кинетическая энергия тела массой m:
где P – импульс тела. 2.8. Теорема о приращении кинетической энергии:
где А12 – работа всех сил, действующих на тело, при перемещении из произвольного положения 1 в произвольное положение 2. 2.9. Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Потенциальная энергия определяется с точностью до некоторой постоянной. Однако это не отображается на физических законах, так как в них входит разность потенциальных энергий в двух положениях тела. Поэтому потенциальную энергию тела в каком–то определенном положении считают равной нулю, а энергию тела в других положениях отсчитывают относительно нулевого уровня.
Потенциальная энергия тела массой m, находящегося на высоте h вблизи поверхности Земли, рассчитывается по формуле U = mgh где под U понимается энергия системы тело-Земля при условии, что нулевой уровень потенциальной энергии находится на поверхности Земли. При упругой деформации х пружины жесткостью k ее потенциальная энергия U =
в предположении, что нулевой уровень потенциальной энергии соответствует недеформированной пружине. Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2, находящихся на расстоянии R друг от друга U = - G где G – гравитационная постоянная. При этом предполагается, что здесь нулевому уровню соответствует потенциальная энергия бесконечно удаленных друг от друга материальных точек. 2.10. Убыль потенциальной энергии тела в поле консервативных сил:
где А12 – работа консервативных сил. 2.11. Закон сохранения механической энергии в поле консервативных сил:
где Е – полная механическая энергия изолированной системы. 2.12. Приращение полной механической энергии тела:
где
|

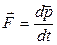 ,
, - результирующая всех внешних сил,
- результирующая всех внешних сил,  - импульс точки (тела).
- импульс точки (тела).
 , тогда сила
, тогда сила  , действующая на тело массой m, равна произведению массы тела на ускорение
, действующая на тело массой m, равна произведению массы тела на ускорение 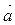 :
: .
.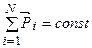
 ,
,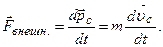
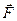 на малом перемещении
на малом перемещении  , в пределах которого сила остается постоянной:
, в пределах которого сила остается постоянной: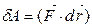 .
.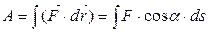 ,
,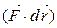 - есть скалярное произведение вектора силы
- есть скалярное произведение вектора силы  на вектор перемещения
на вектор перемещения  ,
,  - элементарный путь,
- элементарный путь, 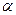 - угол между векторами
- угол между векторами  Для постоянной силы
Для постоянной силы 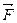 , действующей под неизменным углом α к перемещению
, действующей под неизменным углом α к перемещению  :
: ,
, ).
).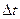 :
: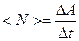 .
. .
. или
или 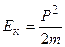 ,
, ,
,
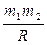 ,
, ,
,
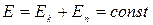 ,
, ,
,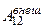 - работа результирующей всех внешних сил, включая работу диссипативных сил, к которым относятся силы трения, сопротивления.
- работа результирующей всех внешних сил, включая работу диссипативных сил, к которым относятся силы трения, сопротивления.


