МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
4.1 Масса молекулы:
где m - молярная масса; NA – число молекул в одном моле. 4.2. Уравнение состояния идеального газа:
где Р – давление газа; V – объем, занимаемый газом; m – масса газа; ( 4.3. Средняя кинетическая энергия молекулы идеального газа:
где k – постоянная Больцмана (k=1,38 Дж/К); i – число степеней свободы молекулы. Здесь мы будем рассматривать только молекулы с жёсткой связью, поэтому i =3 (одноатомный газ), i =5 (двухатомный газ), i =6 (трёх и более атомный газ). 4.4. Основное уравнение кинетической теории газов:
где n – число молекул в единице объема; m0 – масса молекулы; 4.5. Характерные скорости молекул: · средняя квадратичная · средняя арифметическая · наиболее вероятная 4.6. Закон Дальтона для смеси идеальных газов:
где Р – давление смеси; 4.7. Внутренняя энергия идеального газа массой m при температуре Т:
4.8. Молярная теплоемкость газа: · при постоянном объеме · при постоянном давлении 4.9. Связь между молярной и удельной теплоемкостями:
где Сμ – молярная теплоемкость; Суд – удельная теплоемкость. 4.10. Теплоемкость тела (газа):
4.11. Первое начало термодинамики:
где Q - количество теплоты, сообщенное системе (телу); 4.12.Работа газа при изменении его объема от V1 до V2:
4.13. Применение первого начала термодинамики к изопроцессам: · изобарный процесс (р = const),
· изохорический процесс (V = const),
· изотермический процесс (T = const),
· адиабатный процесс,
4.14. Уравнение Пуассона для адиабатного процесса:
где 4.15. КПД тепловой машины:
где Q1 – количество теплоты, получаемое рабочим телом; Q2 - количество теплоты, отдаваемое телом; A – полезная работа, совершаемая рабочим телом. 4.16. Цикл Карно, КПД цикла Карно. Цикл Карно – обратимый круговой процесс,состоящий из двух изотерм и двух адиабат (рис.7), его КПД определяется только температурами нагревателя Т1 и холодильника Т2:
4.17. Средняя длина свободного пробега молекулы газа:
где d – эффективный диаметр молекулы, n – концентрация молекул, <z>; – среднее число столкновений молекулы в единицу времени. 4.18. Явления переноса. ·
где · Для газов коэффициент диффузии:
· Внутреннее трение (вязкость), закон Ньютона:
где F – сила трения между движущимися слоями жидкости или газа (рис.9); газа (или жидкости) вдоль оси х; ·
· Теплопроводность, закон Фурье:
где · æ – коэффициент теплопроводности для газов: æ= В формулах коэффициентов переноса:
Примеры решения задач.
Пример 5. 6 г углекислого газа (CO2) и 5 г закиси азота (N2O) заполняют сосуд объемом 2
Дано: m1 = 6 Найти: р. Решение. В сосуде находится смесь газов. На основании закона Дальтона: р= р1 + р2, (1) где р, р1, р2 - соответственно давление смеси и парциальные давления составляющих смесь газов. Для каждого компонента смеси запишем уравнение Менделеева- Клапейрона:
Выразив давления p1 и p2 из уравнений (2), (3) и подставив полученные соотношения в (1), получим искомое давление смеси:
Выполним вычисления:
Ответ: р = 4,2 Пример 6. Кислород массой 10г находятся под давлением 3
Дано: m =10-2 кг; р =3 Найти: Решение. Используем первое начало термодинамики:
где Внутренняя энергия идеального газа определяется по формуле:
Следовательно, изменение внутренней энергии:
Запишем уравнение Менделеева – Клапейрона для состояния газа до и после расширения:
Разделив уравнение (5) на уравнение (4), получим:
Отсюда
Объем V1 найдем из уравнения (4):
Следовательно,
По формуле (2) найдем U1 и U 2:
Работа расширения газа:
По уравнению (1) найдем Q:
Ответ: U1 = 1,8 103 Дж; U2 = 7,5 103 Дж; Q = 8,0 103 Дж. Пример 6. Коэффициенты диффузии и внутреннего трения водорода при некоторых условиях равны соответственно: D = 1,42 см2/с и
Дано: Найти: n. Решение. Коэффициент динамической вязкости и коэффициент диффузии определяются формулами:
Разделив уравнение (1) на уравнение (2), получим:
Плотность
Массу молекулы выразим через молярную массу:
Ответ: 1,8·1025 м-3.
|

 ,
, ,
, - количество вещества (число молей n); R – универсальная газовая постоянная
- количество вещества (число молей n); R – универсальная газовая постоянная ).
). ,
, ,
, - средняя квадратичная скорость молекул; <Е 0 пост>; - средняя кинетическая энергия поступательного движения молекулы
- средняя квадратичная скорость молекул; <Е 0 пост>; - средняя кинетическая энергия поступательного движения молекулы  .
.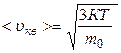 =
=  ;
; =
=  ;
; =
=  .
. ,
, - парциальное давление i – го компонента смеси, т.е. давление, которое оказывает на стенки сосуда каждый из компонентов смеси в отдельности, если бы он занимал объем, равный объему смеси при температуре смеси.
- парциальное давление i – го компонента смеси, т.е. давление, которое оказывает на стенки сосуда каждый из компонентов смеси в отдельности, если бы он занимал объем, равный объему смеси при температуре смеси.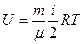 .
. ;
; .
. ,
,
 ,
, - изменение внутренней энергии системы; A – работа, совершаемая системой против внешних сил.
- изменение внутренней энергии системы; A – работа, совершаемая системой против внешних сил. .
. ;
; ,
,  ;
; ,
,  ;
; ,
,  (адиабатное расширение)
(адиабатное расширение) (адиабатное сжатие)
(адиабатное сжатие) ;
;  ;
;  ,
, - показатель адиабаты.
- показатель адиабаты. ,
,
 .
. , Рис.7
, Рис.7 Диффузия, закон Фика:
Диффузия, закон Фика: ,
, - масса, переносимая через площадку S
- масса, переносимая через площадку S  , перпендикулярную оси х за время Δt (рис.8);
, перпендикулярную оси х за время Δt (рис.8);  - градиент плотности вдоль оси х; D – коэффициент диффузии.
- градиент плотности вдоль оси х; D – коэффициент диффузии. .
.
 ,
, – градиент скорости,
– градиент скорости, – коэффициент внутреннего трения (динамической вязкости).
– коэффициент внутреннего трения (динамической вязкости). .
. æ
æ  ,
, - количество теплоты, переносимой через площадку
- количество теплоты, переносимой через площадку  , перпендикулярную оси х, за время Δt;
, перпендикулярную оси х, за время Δt;  - градиент температуры;æ – коэффициент теплопроводности.
- градиент температуры;æ – коэффициент теплопроводности. .
. - средняя арифметическая скорость молекул;
- средняя арифметическая скорость молекул; - средняя длина свободного пробега молекул газа;
- средняя длина свободного пробега молекул газа; - плотность газа;
- плотность газа; - удельная теплоемкость газа при постоянном объеме.
- удельная теплоемкость газа при постоянном объеме. м3. Каково общее давление гза в сосуде при температуре 1270 С?
м3. Каково общее давление гза в сосуде при температуре 1270 С? (2)
(2) (3)
(3) .
. Па.
Па. Па.
Па. U1; U2.
U1; U2. (1)
(1) - изменение внутренней энергии газа (
- изменение внутренней энергии газа ( ); А – работа, совершаемая газом.
); А – работа, совершаемая газом. . (2)
. (2)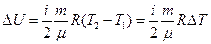 . (3)
. (3) ; (4)
; (4) . (5)
. (5) . (6)
. (6) . (7)
. (7) м3.
м3. К.
К. Дж;
Дж; Дж.
Дж. Дж
Дж Дж.
Дж. Па×с. Найти число молекул водорода в одном м3 при этих условиях (концентрацию молекул).
Па×с. Найти число молекул водорода в одном м3 при этих условиях (концентрацию молекул). ;
; 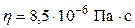 .
.
 , (1)
, (1)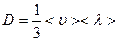 . (2)
. (2) (3)
(3) выразим через концентрацию молекул n и массу одной молекулы m0:
выразим через концентрацию молекул n и массу одной молекулы m0: (4)
(4) (5) Концентрацию n выразим из соотношения (4), заменив плотность соотношением (3), массу молекулы соотношением (5), получим:
(5) Концентрацию n выразим из соотношения (4), заменив плотность соотношением (3), массу молекулы соотношением (5), получим: =
=  м-3.
м-3.


