ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
3.1. Момент силы и момент импульса
Различают момент силы относительно точки (точка О на рис. 3), называемая неподвижным началом или полюсом, и момент силы относительно оси. Моментом силы относительно точки называется векторное произведение радиус-вектора
Модуль вектора М = F Под плечом силы понимается кратчайшее расстояние
Моментом силы относительно произвольной оси называется проекция момента силы относительно точки, находящейся на оси, на эту ось. Моментом импульса материальной точки относительно неподвижного начала называется векторное произведение радиус-вектора
Вектор Модуль вектора момента импульса равен произведению модулей векторов L = rPsin α Моментом импульса относительно произвольной оси называется проекция момента импульса относительно точки, находящейся на оси, на эту ось. Производная по времени t момента импульса
Аналогичное утверждение справедливо и для системы тел или материальных точек, однако здесь под
а под
действующих на такую систему:
3.2. Момент инерции твердого тела относительно данной оси:
где m i и r i - соответственно массы и расстояния материальных точек до оси вращения. 3.3. Моменты инерции относительно оси Z0, проходящей через центр масс перпендикулярно плоскости основания: сплошного цилиндра (диска) радиусом R и массой m Jz0 = полого цилиндра массой m, внутренним радиусом R1 и внешним R2 Jz0 = тонкостенного полого цилиндра (обруча) массой m радиусами R1 Jz0 = mR2. Момент инерции шара массой m и радиусом R относительно оси Z0, проходящей через центр масс Jz0 = Момент инерции тонкого стержня массой m и длиной Jz0 =
3.4. Теорема Штейнера. Момент инерции тела I относительно любой оси равен моменту его инерции Ic относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния d между осями:
3.5. Основное уравнение динамики вращательного движения. Результирующий момент внешних сил относительно оси вращения z равен произведению момента инерции твердого тела относительно этой оси на угловое ускорение:
3.6. Момент импульса
где I z – момент инерции тела относительно оси вращения. 3.7. Закон сохранения момента импульса. · Момент импульса в замкнутой системе тел сохраняется:
· в проекции на ось вращения z:
где 3.8. Кинетическая энергия тела, вращающегося относительно неподвижной оси:
3.9. Работа при повороте твердого тела относительно произвольной неподвижной оси z на некоторый угол φ под действием внешних сил Мz А =
3.10. Кинетическая энергия при плоском движении твёрдого тела:
где
|

 , проведенного из этой точки (рис. 3), в точку приложения силы
, проведенного из этой точки (рис. 3), в точку приложения силы  на эту силу:
на эту силу: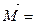 [
[ 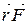 ]
]
 может рассчитываться также как произведение модуля силы
может рассчитываться также как произведение модуля силы 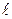 (рис. 3):
(рис. 3):
 , соединяющего неподвижное начало и движущуюся материальную точку, на импульс этой точки:
, соединяющего неподвижное начало и движущуюся материальную точку, на импульс этой точки: = [
= [  ]
] . Направление вектора
. Направление вектора 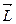 определяется направлением векторного произведения векторов
определяется направлением векторного произведения векторов 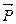 на синус угла между ними:
на синус угла между ними:
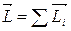 ,
, ,
,
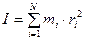 ,
, mR2;
mR2; ;
;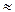 R2
R2  mR2
mR2 m
m 
 .
. .
.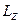 тела относительно оси вращения:
тела относительно оси вращения: ,
, ,
, ,
, - момент импульса i- го тела относительно оси вращения, т.е. проекция момента импульса i- го тела на ось вращения системы.
- момент импульса i- го тела относительно оси вращения, т.е. проекция момента импульса i- го тела на ось вращения системы. .
.
 ,
, - скорость центра масс тела,
- скорость центра масс тела,  - момент инерции тела относительно на оси, проходящий через центр масс тела.
- момент инерции тела относительно на оси, проходящий через центр масс тела.


