Аналитические показатели ряда динамики
На практике для количественной оценки динамики явлений широко применяется ряд основных аналитических показателей. К таким показателям относится, абсолютный прирост. При этом принято сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение – базисным. Абсолютный прирост ( ∆ y – абсолютный прирост – это разность между уровнями ряда динамики. Может быть цепным или базисным:
Показатель интенсивности изменения уровня ряда, в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или темпом роста. Коэффициент роста показывает, во сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы).
либо как базисные, когда все уровни сопоставляются с одним и тем же уровнем, выбранным за базу сравнения (при умножении на 100 – в процентном выражении):
Между цепными и базисными темпами роста существует взаимосвязь: произведение всех цепных темпов роста равно последнему базисному. Тпр – темп прироста – относительный показатель, показывающий, насколько один уровень ряда динамики больше или меньше другого, принимаемого за базу сравнения:
При делении абсолютного прироста (цепного) на темп прироста (цепной) получим показатель, называемый значением одного процента прироста – А:
Пример. Произведем расчет и анализ динамики заключения браков в Омской области за 2000–2003 гг., используя формулы вышеизложенных показателей и данные таблицы 13.5. За базу сравнения примем уровень 2000 года. Таблица 13.5 Показатели изменения уровней ряда динамики
Далее в таблице 13.6 приведем всю совокупность показателей ряда динамики, позволяющую посмотреть взаимосвязи между ними. Таблица 13.6 Показатели изменения уровней ряда динамики
При изучении ряда динамики важно проследить направление и размер изменений уровня ряда во времени. С этой целью для динамических рядов рассчитываются следующие показатели. Среднегодовой темп роста, ориентированный на достижение конечного уровня (yn) в исследуемом периоде, можно рассчитать как среднюю геометрическую из годовых темпов роста по следующим формулам:
Если же ориентация берется на достижение суммарного значения (объема) исследуемого показателя за определенный период, то для расчета среднего коэффициента (темпа) роста используется так называемая средняя параболическая вида
где значение k определяется по специальной таблице для расчета средних коэффициентов роста (снижения) по средней параболической. Пример. Таблица 13.7 Данные о вводе в действие жилой площади в городе N
Определим среднегодовой темп роста ввода в действие жилой площади за 2003–2008 гг. (т.е. за 6 лет), ориентированный на достижение общей суммы введенного жилья за указанный период (т.е. 394,7 млн. кв.м). Решение. Используем формулу (13.8) средней параболической:
далее по таблице для расчета средних коэффициентов роста (снижения) по средней параболической в графе n = 6 находим значение, наиболее близкое к полученному отношению (6,315). Это число 6,323, которому соответствует Пример. Таблица 13.8 Данные о прибыли на предприятии за 2000–2005 гг.
Рассчитаем среднегодовой темп роста (снижения) за 2000–2005 гг., ориентированный: 1) на достижение фактического уровня в 2005 г. по формуле (13.7)
2) на общий объем (за 5 лет), то применим для расчета формулу (13.8). Пример. Имеются данные о численности мужской части населения Омской области за 5 лет на начало года (табл. 13.9):
далее по таблице На практике, т. к. конечный уровень ряда может быть случайным (нехарактерным), чаще применяется расчет по формуле (13.8), где учитывается сумма уровней за n лет. Прогнозирование на основе рядов динамики Суть нижеприведенного способа (выравнивание по аналитическим формулам) заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени, т.е. Таблица 13.9 Численность мужской части населения в 1999–2003 гг. (на 1.01)
Найдем линию тренда и, используя полученное уравнение, сделаем прогноз на будущее (определим численность мужской части населения в Омской области в 2006 году). Предположим, что численность населения изменяется во времени по прямой:
Для нахождения параметров а0 и а1 решим систему нормальных уравнений, отвечающих требованию способа наименьших квадратов
Далее в таблице 13.12 рассчитаны необходимые для решения системы уравнения суммы: ∑, ∑ t, ∑ t2, ∑ yt. Годы последовательно обозначим как 1, 2, 3, 4, 5 (n = 5). Таблица 13.10 Расчетные данные для определения параметров уравнения тренда
Из системы уравнений получим a 1 = −9,85; а 0 = 1039,35; Отсюда искомое уравнение тренда Для 2006 года t = 8; следовательно, Для решения данной задачи можно использовать и второй способ, упрощенный. Если время t обозначить так, чтобы ∑ t = 0, т. е. счет вести от середины ряда, то система упростится и примет вид
В этом случае каждое уравнение решается самостоятельно:
Необходимые для расчета параметров уравнения суммы приведем в таблице 13.11. Таблица 13.11 Расчетные данные для определения параметров уравнения тренда
Тогда Уравнение тренда в этом случае будет имеет вид Для 2006 г. t = 5; следовательно, Эта величина условная, рассчитанная при предположении, что линейная закономерность изменения численности мужской части населения, принятая для 1999–2003 гг., сохранится на последующий период до 2006 г. Контрольное задание По данным статистических ежегодных изданий: «Российский статистический ежегодник», «Россия в цифрах» и т.п. выберите несколько показателей, постройте и проанализируйте ряды динамики, найдите линию тренда и, используя полученное уравнение, сделайте прогноз на 3 года вперед.
|

 ) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста. В общем случае абсолютный прирост может быть представлен в виде:
) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста. В общем случае абсолютный прирост может быть представлен в виде: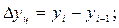 (13.1)
(13.1) (13.2)
(13.2) – темп роста – относительный показатель, получающийся в результате сопоставления двух уровней одного ряда динамики. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем:
– темп роста – относительный показатель, получающийся в результате сопоставления двух уровней одного ряда динамики. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем: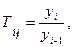 (13.3)
(13.3) (13.4)
(13.4) или
или  (13.5)
(13.5) (13.6)
(13.6)

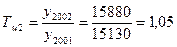

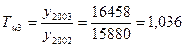
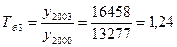


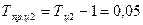



 (13.7)
(13.7) (13.8)
(13.8)
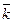 =1,015. Это искомый среднегодовой коэффициент роста ввода жилья за 6 лет. Отсюда, среднегодовой темп роста ввода в действие жилой площади за указанный период составлял 101,5 %, а среднегодовой темп прироста был равен
=1,015. Это искомый среднегодовой коэффициент роста ввода жилья за 6 лет. Отсюда, среднегодовой темп роста ввода в действие жилой площади за указанный период составлял 101,5 %, а среднегодовой темп прироста был равен  или 91,7 %, т.е. ежегодно объем прибыли уменьшался в среднем на 8,3 %;
или 91,7 %, т.е. ежегодно объем прибыли уменьшался в среднем на 8,3 %;

 (13.9)
(13.9)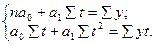 (13.10)
(13.10)
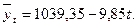
 То есть по прогнозу численность мужской части населения в Омской области в 2006 году составит 960,55 тыс. чел.
То есть по прогнозу численность мужской части населения в Омской области в 2006 году составит 960,55 тыс. чел.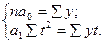 (13.11)
(13.11) (13.12)
(13.12)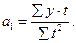 (13.13)
(13.13)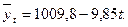
 и
и 




