Метод Квайна минимизации булевых функций
Предположим, что функция задана в ДСНФ. Элементарные конъюнкции ранга n будем называть минитермами ранга n. Шаг 1. Нахождение первичных импликант. Все минитермы данной ФАЛ сравниваются между собой попарно. Если минитермы Минитермы Замечание. Если в конце первого шага остаються неотмеченные минитермы ранга Для заданной ФАЛ первуй шаг заканчивается построением сокращенной ДНФ:
где Шаг 2. Формирование импликантной таблицы Для нахождения минимального покрытия интервалами максимального ранга не обходимо выполнить удаление некоторого количества первичных импликант. На втором шаге формируется таблица, число строк в таблице равно числу первичных импликанты, а число столбцов равно числу минитермов исходной ДСНФ. Если некоторая импликанта покрывает или поглощает определенный минитерм ДСНФ, то в импликантной таблице на пересечении соответствующих строк и столбцов ставится метка. Шаг 3. Нахождение существенных импликант Если в определенном столбце расположена ровно одна метка, то соответствующая импликанта называется существенной. Существенная импликанта не может бать удалена из правой части (1), потому что без нее не будет получено покрытие всего множества Шаг 4. Вычеркивание лишних столбцов Если в таблице есть два столбца с одинаковыми метками в одних и тех же строчках, то один из них вычеркивается (так как покрытие одного из них обеспечивает и покрытие другого). Шаг 5. Вычеркивание лишних первичных импликант Если после этапа 4 в таблице есть строки без единой метки, то они вычеркиваются. Шаг 6. Выбор минимального покрытия максимальными интервалами Исследуется полученная таблица: выбирается такая совокупность первичных импликант, которая включает метки во всех столбцах (по крайней мере по 1 в каждом столбце). При нескольких вариантах отдается предпочтение варианту покрытия с минимальным суммарным с минимальным суммарным числом букв в простых импликантах.
Метод Мак-Класки минимизации булевых функций Метод Мак-Класки - модификация первого этапа метода Квайна. Шаг 1. Всем минитермам ставим в соответствие их двоичный эквивалент.
Шаг 2. Все номера-минитермы разбиваем на группы по числу единиц в этих номерах. Шаг 3. Все минитермы сравниваются между собой попарно. Попарное сравнение можно производить только между соседними группами, т.к. только эти группы отличаются для входящих в них минитермов в одном разряде. Шаг 4. Преобразование новых минитермов: В разрядах, соответствующих исключенным переменным, ставим черточку. Такая модификация удобна еще и отсутствием громоздкой записи.
Шаг 5. Строим таблицу и расставляем метки, как и в методе Квайна (п.2). Шаг 6. Далее минимизация проводится по таблице как и в методе Квайна (п.3-6). Например: Задана функция f(x1,x2,x3,x4,), которая равна единице на наборах с номерами – 0, 1, 2, 3, 4, 6, 7, 8, 9, 11, 15. Минимизировать ее методом Квайна - Мак-Класки. Решение: 1. Построим двоичные наборы, на которых задана функция.
2. Разобьем минитермы на группы по числу единиц. 0000* ------------------------------ – нулевая группа 0001*, 0010*, 0100*, 1000* --- – первая группа 0011*, 0110*, 1001* ------------ – вторая группа 0111*, 1011* --------------------- – третья группа 1111* ------------------------------ – четвертая группа
3. Сравним все минитермы попарно между собой, и произведем преобразование. Полученные минитермы также разобьем на группы. 000_*, 00_0*, 0_00*, _000* ----------------- – нулевая группа 00_1*, _001*, 001_*, 0_10*, 01_0*, 100_* – первая группа 0_11*, _011*, 011*_, 10_1* ----------------- – вторая группа _111*, 1_11* ----------------------------------- – третья группа
4. Продолжим сравнение и преобразование минитермов до тех пор пока преобразование станет невозможным. 00_ _, _00 _, 0__0 ---------------- – нулевая группа _0_1, 0_1_ ------------------------ – первая группа _ _11 ------------------------------- – вторая группа
5. Построим таблицу и расставим метки. 6.
7. Проведем преобразования таблицы (п. 3-6 метода Квайна). Вычеркиваем столбцы, соответствующие существенным импликантам и отметим (●) столбцы минитермов, покрываемых ими.
8. Выберем совокупность первичных импликант, которая включает метки во всех столбцах (по крайней мере по 1 в каждом столбце).
В результате получаем
|
и 
таковы, что их можно попарно представить в виде 
, то выписывается конъюнкция, которая является минитермом ранга 
: 
.
-го ранга, для которых произошло склеивание отмечаются (*). После построения всех минитермов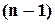 
-го ранга вновь сравнивают их попарно, выписывают минитермы 
-го ранга и отмечают склеивающиеся минитермы и т.д. Этап заканчивается, когда вновь полученные минитермы 
-го ранга уже не склеиваются между собой. Все неотмеченные минитермы называются первичными или простыми импликантами.
, то их можно сразу вписать в минимальную форму, поскольку дальше они будут только усложнять выполнение алгоритма.
,
- есть первичные импликанты.
данной функции. Поэтому из таблицы меток исключаем строки соответствующие существенным импликантам, и столбцы минитермов, покрываемые ими. Сами существенные импликанты вписываются в минимальную форму.
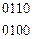
00__
