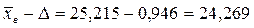Задача 3. Для оценки стоимости основных фондов региона произведен 5% механический отбор, в результате чего установлено: Группы предприятий по стоимости основных
Для оценки стоимости основных фондов региона произведен 5% механический отбор, в результате чего установлено:
По включенным в выборку предприятиям определите: ú Среднюю стоимость основных фондов на 1 предприятие ú Среднее квадратическое отклонение. ú Долю предприятий со стоимостью основных фондов более 50 млн. руб. ú С вероятностью 0,954 пределы, в которых можно ожидать среднюю стоимость основных фондов на 1 предприятие. ú С вероятность 0,997 долю предприятий, со стоимостью основных фондов выше 50 млн. руб.
Решение.
Закроем открытые интервалы (1-ый и 6-ой), считая, что шаг интервала постоянный и равен 10. Определим числовые характеристики выборки: Таблица 3.1
xi – середина интервала, ni – частота, Относительная частота:
Выборочное среднее:
Выборочная дисперсия:
Выборочное среднее квадратическое отклонение:
Теперь известно, что:
σx =15,357 σx2 =235,829 n =1000 – объем выборки,
N – объем генеральной совокупности. Средняя ошибка механической выборки для среднего значения определяется по формуле ошибки случайной бесповторной выборки: Предельная ошибка выборки для среднего значения:
Где t – кратность ошибки, зависит от доверительной вероятности. p =0.954, Ф(t)=p - функция Лапласа. Определяем аргумент функции Лапласа по таблице приложения. Ф (2)=0,954, следовательно t =2. Пределы, млн. руб.:
Средняя ошибка механической выборки для доли:
w =0.074 - доля предприятий со стоимостью основных фондов выше 50 млн. руб.
Предельная ошибка выборки для доли:
t – кратность ошибки, зависит от доверительной вероятности. p =0.997, Ф(t)=p - функция Лапласа. Определяем аргумент функции Лапласа по таблице приложения. Ф (3)=0,997, следовательно t =3 Пределы для доли, доля 1:
или 6,6%
или 8,2% Делаем вывод. ú Средняя стоимость основных фондов на одно предприятие в генеральной совокупности с вероятностью 0,954 находится в пределах: от 24,269 до 26,161 млн. руб. ú С вероятностью 0,997 в генеральной совокупности пределы для доли предприятий со стоимость основных фондов выше 50 млн. руб. составляют: от 6,6% до 8,2%.
|






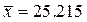
 - т. к. выборка 5%,
- т. к. выборка 5%,