Общие сведения
Гидравлический расчёт трубопровода с насосной подачей основан на применении уравнения Бернулли, которое в общем случае имеет вид:
где z 1(2) – геометрическая высота (геометрический напор), м;
р 1(2) – избыточное давление, МПа; ρ; – плотность жидкости, кг/м3;
α;1(2) – коэффициент Кориолиса (для ламинарного режима течения жидкости α; = 2, для турбулентного – α; = 1);
h пот – потери напора, м. Напор – это удельная (то есть отнесённая к единице веса) энергия жидкости. Согласно уравнению Бернулли (1), полный напор Н – это сумма геометрического, пъезометрического и скоростного напоров в данном сечении:
Уравнение Бернулли применяют для расчёта простого неразветвлённого трубопровода, и равенство полных напоров (геометрического, пъезометрического и скоростного) для двух сечений рассматривают с учётом потерь напора h пот, которые всегда находятся в правой части уравнения со знаком ″+″: Н 1 = Н 2 + h пот. (3) Потери напора h пот – это потери энергии на участке от сечения 1 – 1 до сечения 2 – 2. Энергия расходуется на преодоление сил трения по длине потока, возникающих при течении жидкости, и теряется на вихреобразование при изменении направления потока жидкости в местных сопротивлениях:
где
Потери напора по трубопроводу длиной l и диаметром d определяют по формуле Дарси – Вейсбаха:
где λ; (ламбда) – коэффициент Дарси, значение которого определяют в зависимости от числа Рейнольдса. Режим течения жидкости (число Рейнольдса) зависит от внутреннего диаметра трубопровода d, средней скорости течения жидкости
При ламинарном режиме течения жидкости (Re < 2300) коэффициент Дарси равен λ;л = 64/ Re, и после его подстановки в формулу (5) потери напора по длине определяют по формуле Пуазейля:
где Q – расход жидкости, м3/c. Местные потери напора при ламинарном режиме течения малы, и их принимают эквивалентными потерям по длине, то есть потери в одном местном сопротивлении или сумма потерь во всех местных сопротивлениях будет равна потерям по некоторой эквивалентной длине l экв, и тогда формула (7) примет вид:
При турбулентном режиме течения жидкости (Re > 2300) для машиностроительных гидроприводов коэффициент λ;т определяют по формуле Блазиуса:
Местные потери напора при турбулентном режиме задают коэффициентом ζ;м (дзэта) местного сопротивления, который указывает количество скоростных напоров, потерянных в данном местном сопротивлении. Потери напора в местном сопротивлении определяют по формуле Вейсбаха: h м = ζ;м Местные потери происходят в гидроаппаратах, необходимых для нормального функционирования систем гидропривода (обратные клапана, распределители, дроссели, клапаны давления), и во вспомогательных устройствах (фильтры, теплообменники). Гидроаппараты по своему назначению разделяют на: - направляющие, основной задачей которых является изменение направления потока рабочей жидкости (обратные клапана, направляющие гидрораспределители); - регулирующие, основной задачей которых является регулирование величин подачи Q и давления р потока рабочей жидкости за счёт изменения проходного (рабочего) сечения гидроаппарата (дроссели, предохранительные и редукционные клапана, регуляторы и синхронизаторы расхода). Условные обозначения элементов гидропривода приведены в табл. 1 приложения. Регулирующие гидроаппараты характеризуются возможностью значительного падения давления. Рассмотрим это на примере нерегулируемого дроссельного клапана (рис. 2).
Рис. 2. Схема установки дросселя (дроссельной шайбы): 1, 2 – манометры; 3 – дроссельная шайба
Величина потери энергии, которая происходит вследствие вихреобразования, будет зависеть от диаметра d 0 проходного сечения дроссельной шайбы. Безусловно, давление р 1 > р 2, и потери энергии можно выразить как перепад давления ∆ р на дросселе: ∆ р = р 1 – р 2. Расход жидкости будет также зависеть от диаметра d 0 – чем меньше диаметр, тем меньше расход, и наоборот. Формула, связывающая перепад давления ∆ р, расход жидкости Q и площадь проходного сечения S 0 =
где μ;р – коэффициент расхода. Коэффициент μ;р определяют по графику, изображённому на рис. 1 приложения, в зависимости от числа Рейнольдса (6). Для машиностроительных объёмных гидроприводов характерны следующие утверждения: - геометрической высотой и скоростным напором пренебрегают, так как величина этих напоров пренебрежительно мала в сравнении с напором пъезометрическим. Рассмотрим это утверждение на примере гидропривода механизма подъёма кузова автомобиля ″КамАЗ″ (рис. 3). Давление насоса гидропривода составляет р н = 16 МПа, высота от линии установки насоса до максимальной линии подъёма жидкости в гидроцилиндре z ≈ 4 м, максимальная скорость потока жидкости по трубопроводу
Рис. 3. Схема гидропривода механизма подъёма кузова автомобиля: 1 – гидроцилиндр; 2 – трубопроводы; Н – насос; КОМ – коробка отбора мощности
Определим значения напоров: - геометрический напор z = 4 м; - пъезометрический напор - скоростной напор Таким образом, значениями геометрического и скоростного напоров можно пренебречь; - потери напора выражают как потери давления ∆ р. При этом среднюю скорость потока выражают через расход в соответствии с уравнением расхода:
Потери напора h пот выразим как:
Тогда формула (5) для определения потерь напора по длине трубопровода при турбулентном движении с учётом (12) и (13) примет вид:
Формула (7) для определения потерь напора по длине при ламинарном режиме с учётом (13) примет вид:
Формула (10) для определения потерь напора в местных сопротивлениях с учётом (12) и (13) примет вид:
∆ р м = ζ;м Формулу (15) применяют, если местное гидравлическое сопротивление задано коэффициентом ζ;м. Если местное сопротивление задано площадью проходного сечения S 0 и коэффициентом расхода μ;р, то в этом случае потери ∆ р м выражают из формулы (11):
Формула (8) для определения потерь напора в местных сопротивлениях при ламинарном режиме движения жидкости с учётом (13) примет вид:
Формулы (15) и (18) идентичны, поэтому общие потери давления на участке длиной l и диаметром d с расположенными на этой длине местными сопротивлениями при ламинарном режиме движения можно выразить формулой:
Очевидно, что формулы (14), (15), (16), (17), (18) и (19) можно представить в виде: ∆ р = KQm, m = 1 или m = 2. (20) Формулы для определения потерь напора по длине и в местных сопротивлениях с учётом общей формы (20) сведём в табл. 1. Таблица 1
|

 , (1)
, (1) – пъезометрическая высота (пъезометрический напор), м;
– пъезометрическая высота (пъезометрический напор), м; – скоростная высота (скоростной напор), м;
– скоростная высота (скоростной напор), м; – средняя скорость потока рабочей жидкости, м/c;
– средняя скорость потока рабочей жидкости, м/c;
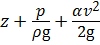 . (2)
. (2) (4)
(4)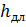 – потери напора по длине потока на участке трубопровода длиной l и диаметром d, м;
– потери напора по длине потока на участке трубопровода длиной l и диаметром d, м;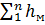 – сумма местных потерь напора, возникающих в местных сопротивлениях количеством n, и расположенных на участке длиной l, м.
– сумма местных потерь напора, возникающих в местных сопротивлениях количеством n, и расположенных на участке длиной l, м. , (5)
, (5) и от её кинематической вязкости ν;:
и от её кинематической вязкости ν;: . (6)
. (6) , (7)
, (7) . (8)
. (8) . (9)
. (9) . (10)
. (10)
 , через которое происходит истечение, называют формулой Торричелли:
, через которое происходит истечение, называют формулой Торричелли: , (11)
, (11) ≈ 4 м/с.
≈ 4 м/с.
 = 2041 м;
= 2041 м; = 0,82 м.
= 0,82 м. , откуда
, откуда  . (12)
. (12) . (13)
. (13) , откуда
, откуда . (14)
. (14) , откуда
, откуда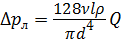 . (15)
. (15) = ζ;
= ζ;  , откуда
, откуда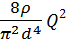 . (16)
. (16) . (17)
. (17) . (18)
. (18) . (19)
. (19)


