Оцінка параметрів моделі з лаговими значеннями показників
1. Для багатьох економічних процесів типовим є те, що ефект від впливу деякого фактора на показник, який характеризує процес, виявляється не одразу, а поступово, через деякий період часу. Таке явище називається лагом (запізненням). Потреба враховувати лаг при кількісному вимірюванні взаємозв’язку між економічними показниками постає дуже часто. Наприклад, у динамічних моделях необхідно враховувати лаг при визначенні зв’язку між обсягом продукції і капітальними вкладеннями, або частину цього лагу – будівельний. Кількісне вираження взаємозв’язку між капітальними вкладеннями і введенням основних фондів, між витратами виробничих ресурсів і обсягом виробництва, між доходами і витратами тощо має базуватися на врахуванні впливу запізнення, або лагу. Причому вплив деяких пояснювальних змінних на залежну може проявлятися не лише через певний період часу, а й протягом певного часу, тобто лаг може складатись з кількох часових періодів. У такому разі маємо справу з економетричною моделлю розподіленого лагу. 2. Нехай економетрична модель розподіленого лагу визначається так:
де Означення. Модель (1) називається загальною моделлю нескінченого розподіленого лагу, якщо для неї справджуються такі умови: 1) 2) 3) 4) 5) Означення 2. Коефіцієнти Означення 3. Якщо виконуються умови (3) – (6), то величини Моделі розподілених лагів можуть задовільно описувати процеси лише в тому разі, коли забезпечена відносна стабільність умов, в яких ці процеси реалізуються. Може йтися про стабільність відповідних індексів цін, процентних ставок за кредити, норми амортизації, термінів будівництва, обсягу та структури ресурсів. Така стабільність далеко не завжди спостерігається для порівняно довгих проміжків часу, протягом яких формується сукупність спостережень. Усе це підводить до побудови узагальненої моделі розподіленого лагу, яка містить не лише лагові змінні, а й інші фактори – пояснювальні змінні Узагальнена модель розподіленого лагу задаватиметься рівнянням
Труднощі оцінювання параметрів такої моделі пов’язані з необхідністю враховувати обмеження на параметри 3. Теоретично побудову моделі з розподіленими лагами можна узагальнити на будь-яку кількість незалежних змінних Як правило, до моделі входять такі змінні
Для різних значень t на основі взаємної кореляційної функції можна дістати n + 1 значення Величину t називають зрушенням (зсуненням). Зрушення, якому відповідає найбільший коефіцієнт взаємної кореляції, називається часовим запізненням, або часовим лагом. Графік нормованої кореляційної функції називається корелограмою. 3. Наявність мультиколінеарності між лаговими змінними утруднює побудову економетричної моделі з лаговими змінними. Один зі способів звільнитись від мультиколінеарності – це ввести такі коефіцієнти при лагових змінних, які мали б однаковий знак і для них можна було знайти суму. З врахуванням умов (3) – (6), модель з розподіленим лагом набере такого вигляду:
Л. Койк запропонував вибрати для запису вагових коефіцієнтів форму спадної геометричної прогресії
де Звідси
Якщо через D позначити оператор зрушення, такий, що Dxt = xt– 1, D 2 xt = xt– 2і т.д., то вираз (10) можна записати так:
З урахуванням цього модель (11) матиме вигляд:
Це припущення, що його зробив Койк, приводить до значних спрощень співвідношення (1). Адже замість оцінки цілого ряду параметрів моделі Діставши оцінку параметра
Входження до формули (11) лагового значення змінної Y має забезпечити досить добру апроксимацію моделі. При цьому слід зауважити, що не завжди лаги розподілятимуться обов’язково за законом Койка, який забезпечує найближчому значенню X найбільшу вагу, а всім наступним – постійно спадні ваги. Якщо можна припустити, що це не так, то тоді лишається кілька перших вагових коефіцієнтів вільними, а для всіх інших використовується закон розподілу Койка. Наприклад, можна записати
де перші два коефіцієнти лишаються вільними, а починаючи з Рівняння (10.13) можна подати у вигляді
Якщо модель має дві пояснювальні змінні, скажімо, х і z, то розподілені лаги Койка можуть бути використані для кожної з них. Найпростіше припустити, що для обох змінних вибирається однакове значення Тоді модель розподіленого лагу
Якщо взяти параметри λ різними для різних пояснювальних змінних, то до моделі треба ввести змінні xt, Zt, yt з оператором
Отже, припущення, зроблене Койком, спричинюється до появи в правій частині рівняння величин Зі щойно сказаного випливає: коли використовувати схему Койка для економетричної моделі, яка має лагові пояснювальні змінні, то в правій частині моделі серед таких змінних з’являється лагова залежна змінна yt– t. З її появою стають стохастичними пояснювальні змінні моделі. До появи в правій частині моделі лагових значень залежної змінної приводять і деякі інші моделі. Добре відомими моделями такого типу є модель часткового коригування і модель адаптивних сподівань. Коли відсутнє повне уявлення про об’єкт, його інерційність, то застосовується метод часткового коригування. Розглянемо його. Нехай
У цьому рівнянні
яка вказує, що протягом поточного періоду часу буде пройдено лише частину відстані між вихідним станом
Ця залежність дуже схожа на кінцеве рівняння Койка (11) і відрізняється лише наявністю вільного члена і простішою формою залишків. Недоліком моделі часткового коригування є те, що оптимальне значення Якщо значення xt змінюється від періоду до періоду, то оптимальне значення також змінюватиметься. Це явище знайшло своє відображення в моделі адаптивних сподівань, яка характеризує зв’язок змінної Y з очікуваним рівнем X. Позначимо його через
де Оскільки Загальноприйнятими в такому разі є припущення про адаптивні сподівання, які можна записати так:
Це означає, що змінні, які спостерігатимуться протягом поточного періоду порівняно з очікуваними раніше, ураховуються лише частково, що й відображує у формулі (18) додатне число
де Використовуючи оператор зрушення D, можна записати:
Підставимо це значення
помноживши обидві частини на
або
Остаточно це рівняння матиме вигляд
Останнє рівняння є простоюмоделлю адаптивних сподівань. Порівнявши його з (16), побачимо, що воно має такі самі змінні, як і модель часткового коригування, відрізняється лише формуванням залишків. Модель адаптивних сподівань відрізняється від схеми Койка лише наявністю вільного члена. Остаточні рівняння всіх трьох моделей практично збігаються, бо як у моделі адаптивних сподівань, так і в моделі часткового коригування використовуються вагові коефіцієнти, що спадають за геометричною прогресією. 4. Коли схема формування вагових коефіцієнтів задовольняє припущення Койка, модель часткового коригування або модель адаптивних сподівань, то у правій частині економетричної моделі виникає лагове значення залежної змінної Y. Це зумовлює певні проблеми при оцінюванні параметрів такої моделі. Розглянемо ці проблеми. Нехай економетрична модель має вигляд
Як ми вже переконалися, методи оцінювання параметрів моделі залежать від гіпотез, які будуть прийняті щодо залишків Гіпотеза 1. Залишки є випадковими величинами і розподіляються нормально, тобто Гіпотеза 2. Залишки виражені через параметр
а) б) Гіпотеза 3. Залишки Перша гіпотеза найпростіша, а тому єдина складність в оцінюванні параметрів моделі пов’язується з наявністю в правій частині лагової змінної Друга гіпотеза відповідає схемі Койка і моделі адаптивних сподівань. При цьому розглядаються два варіанти: а) залишки б) залишки Третя гіпотеза не пов’язується ні зі схемою Койка, ні з моделлю адаптивних сподівань. Згідно з цією гіпотезою величина залишків Розглянемо особливості оцінки параметрів моделі при різних гіпотезах відносно залишків. Гіпотеза 1. Оскільки залишки не корельовані між собою, то оцінка параметрів може бути виконана за методом 1МНК. Але цей метод дасть зміщення оцінки, бо залишки не можна вважати незалежними від лагової змінної Щоб знайти величину зміщення розглянемо таку модель:
де Для такої моделі оцінка параметрів a на основі 1МНК дає
В економетричній літературі доведено, що в такому разі зміщення параметра
Альтернативною оцінкою параметра a може слугувати коефіцієнт автокореляції першого порядку для у, тобто
Зміщення тоді визначатиметься так:
тобто обидві оцінки мають тенденцію до завищення параметра a, причому рівень зміщення параметра r більший, ніж параметра За допомогою методу Монте-Карло було досліджено оцінки параметрів a у моделі а) визначення параметра r; б) використання параметра r, скоригованого на величину зміщення в (21); в) застосування 1МНК. При цьому виявилось, що оцінка параметрів a на основі 1МНК має найменшу середньоквадратичну помилку. Звідси, якщо залишки рандомізовані, то найдоцільніше використовувати 1МНК. Гіпотеза 2а. Якщо залишки в моделях з лаговою змінною
Асимптотичні зміщення оцінки
тобто асимптотичне зміщення для критерію Дарбіна–Уотсона – це подвоєне зміщення для оцінки параметра Коли в економетричній моделі серед пояснювальних змінних є лагове значення залежної змінної, застосування критерію Дарбіна– Уотсона для виявлення серійної кореляції залишків приводить до зміщення його оцінок. Тому Дарбін розробив методи перевірки автокореляції залишків, які можна застосувати і для моделей з лаговими змінними, що побудовані на базі великих сукупностей спостережень (n). Цей критерій визначається так:
де ut=ut– 1 +ut, var
Для перевірки нульової гіпотези обчислені величини h порівнюються з критичними значеннями (односторонній критерій) нормального розподілу (c2) при вибраному рівні значущості. З формули цього критерію видно, що коли var Розглянемо особливості оцінки параметрів, коли залишки мають форму для моделі адаптивних сподівань і схеми Койка, тобто Тоді математичне сподівання залишків дорівнюватиме нулю
Оскільки дисперсія залишків пропорційна до величини 1 + l2, тоді як коваріація для t = ±1 дорівнює –ls2, а для ½t½ ³ 2 дорівнює нулю, то матриця V має вигляд
а матриця X містить лагову змінну Узявши до уваги, що параметр
Тоді матриця X складатиметься лише з двох стовпців, перший з яких утворюється одиницями, а другий – спостереженнями над X. Вектор Y в такому разі складається з перетворених даних Зельнер і Гейсел запропонували вибирати значення параметра з інтервалу: 0 < Гіпотеза 2б. Згідно з цією гіпотезою залишки мають вигляд:
Зельнер і Гейсел запропонували процедуру пошуку параметрів l і Запишемо економетричну модель (25) у вигляді
Визначимо
Перепишемо це рівняння так:
де Оскільки
то
Шляхом послідовних підстановок можна записати
Якщо l і
З огляду на те, що l і Як бачимо, процедура оцінювання параметрів при гіпотезах 2а і 2б є досить громіздкою. Тому використовувати її слід лише тоді, коли є впевненість, що залишки мають ту специфікацію, яка визначає особливості прийнятої гіпотези. Гіпотеза 3. Згідно з цією гіпотезою специфікується модель:
де Ця гіпотеза не пов’язується ні зі схемою Койка, ні з моделлю адаптивних сподівань. Ідеться про оцінку параметрів моделі, яка має серед пояснювальних змінних лагове значення залежної змінної і одночасно має автокорельовані залишки. Розглянемо метод Ейткена. Якщо
і оцінити параметри моделі за методом Ейткена:
де Така процедура наближено еквівалентна застосуванню 1МНК до моделі
відносно перетворених даних. У результаті дістаємо обґрунтовані і асимптотично ефективні оцінки параметрів, але через присутність лагового значення залежної змінної в правій частині, вони будуть зміщеними для кінцевих вибірок. Якщо значення параметра Як альтернативу можна запропонувати ітеративний метод. Розглянемо його. Перепишемо останнє рівняння у вигляді:
Щоб безпосередньо оцінити всі чотири параметри мінімізацією суми квадратів відхилень для (28), треба розв’язувати нелінійні рівняння відносно параметрів. Якщо розбити параметри на дві множини, внісши до однієї a 0, a 1, a 2, а до іншої –
|

 , (1)
, (1)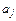 – параметри моделі при лагових змінних;
– параметри моделі при лагових змінних;  – пояснювальна лагова змінна; t – період зрушення;
– пояснювальна лагова змінна; t – період зрушення;  – залишки, що розподілені нормально, тобто мають нульове математичне сподівання і сталу дисперсію.
– залишки, що розподілені нормально, тобто мають нульове математичне сподівання і сталу дисперсію. , для будь-яких k, j; (2)
, для будь-яких k, j; (2) , j = 1, 2, 3...; k = 1, 2, 3...; (3)
, j = 1, 2, 3...; k = 1, 2, 3...; (3) , де w – скінченне число; (4)
, де w – скінченне число; (4) ; (5)
; (5) ,
, 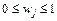 . (6)
. (6)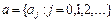 – структурою лагу.
– структурою лагу. називаються нормованими коефіцієнтами лагу, а послідовність
називаються нормованими коефіцієнтами лагу, а послідовність  – нормованою структурою лагу для моделі (1).
– нормованою структурою лагу для моделі (1). , значення яких характеризують поточні умови функціонування економічних систем у період t.
, значення яких характеризують поточні умови функціонування економічних систем у період t. . (7)
. (7)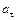 .
. . Але практична реалізація такої моделі часто стикається з непереборними труднощами, що зумовлені великою кількістю факторів, істотною обмеженістю часових рядів і складністю їх внутрішньої структури.
. Але практична реалізація такої моделі часто стикається з непереборними труднощами, що зумовлені великою кількістю факторів, істотною обмеженістю часових рядів і складністю їх внутрішньої структури. з елементом вектора незалежної
з елементом вектора незалежної  , зсунутим один відносно одного на часовий лаг t.
, зсунутим один відносно одного на часовий лаг t. . (8)
. (8) . Якщо t = 0, то маємо парний коефіцієнт кореляції. Значення
. Якщо t = 0, то маємо парний коефіцієнт кореляції. Значення  . Найбільше значення
. Найбільше значення  . (9)
. (9) , (10)
, (10) .
. . (11)
. (11) .
. .
. і
і  у рівнянні, де
у рівнянні, де  .
. , тому для геометричного розподілу середній лаг
, тому для геометричного розподілу середній лаг .
. (12)
(12) вони спадають геометрично. Використаємо оператор зрушення D для скороченого запису моделі (10.13).
вони спадають геометрично. Використаємо оператор зрушення D для скороченого запису моделі (10.13). (13)
(13) .
.
 . причому для змінної
. причому для змінної 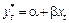 . (14)
. (14) розглядається як оптимальне значення yt, яке відповідає xt. Так, наприклад, якщо xt – дохід, то yt може визначати величину оптимальних витрат при доході xt. Нехай величина доходу xt різко змінюється (збільшується чи зменшується). При цьому споживчі витрати yt можуть не змінитись адекватно доходу з різних причин: певна інерційність, недостатня інформація, договірні умови і т.ін. Тому в даному разі використаємо коригуючу функцію:
розглядається як оптимальне значення yt, яке відповідає xt. Так, наприклад, якщо xt – дохід, то yt може визначати величину оптимальних витрат при доході xt. Нехай величина доходу xt різко змінюється (збільшується чи зменшується). При цьому споживчі витрати yt можуть не змінитись адекватно доходу з різних причин: певна інерційність, недостатня інформація, договірні умови і т.ін. Тому в даному разі використаємо коригуючу функцію: , (15)
, (15) . (16)
. (16)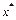 . Маємо
. Маємо , (17)
, (17) – очікуване значення xt, яке сформоване в поточний момент часу, ut – залишки, які можуть бути пов’язані з неточним вимірюванням значення змінної
– очікуване значення xt, яке сформоване в поточний момент часу, ut – залишки, які можуть бути пов’язані з неточним вимірюванням значення змінної  .
. . (18)
. (18) , яке не перевищує одиниці. Щоб перейти до змінних
, яке не перевищує одиниці. Щоб перейти до змінних  ,
, .
. .
. ,
, дістанемо:
дістанемо: ,
,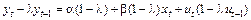 .
. .
. . (19)
. (19) .
. .
. .
. ,
, 
 .
. ,
,  ,
,  .
. описується авторегресійною схемою першого порядку (найпростіший випадок).
описується авторегресійною схемою першого порядку (найпростіший випадок).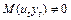 , то і
, то і  для
для  і
і  .
. ,
, і послідовні значення
і послідовні значення  .
.
 . (19)
. (19) . (20)
. (20) , (21)
, (21) де
де  то оцінки параметрів моделі 1МНК матимуть зміщення. Так, якщо
то оцінки параметрів моделі 1МНК матимуть зміщення. Так, якщо 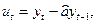 то зміщення для
то зміщення для  буде
буде . (22)
. (22) , (23)
, (23) .
. ,
, – оцінка параметра в автокореляційній моделі першого порядку:
– оцінка параметра в автокореляційній моделі першого порядку: – оцінка вибіркової дисперсії параметра
– оцінка вибіркової дисперсії параметра 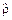 можна дістати з такого співвідношення:
можна дістати з такого співвідношення: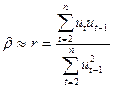 .
. ,
,  .
.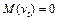 для всіх t, а дисперсія визначатиметься так:
для всіх t, а дисперсія визначатиметься так: 
 для всіх t. А це означає, що для оцінювання параметрів моделі в даному разі можна використати узагальнений метод найменших квадратів:
для всіх t. А це означає, що для оцінювання параметрів моделі в даному разі можна використати узагальнений метод найменших квадратів: .
. , (24)
, (24)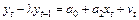 . (25)
. (25) . Як бачимо, проблема оцінювання параметрів у цьому випадку зводиться до знаходження параметра l.
. Як бачимо, проблема оцінювання параметрів у цьому випадку зводиться до знаходження параметра l. < 1. Це означає, що довільно вибирається параметр l, на основі якого формується матриця V з (24). Ця матриця в свою чергу дає змогу знайти оцінки параметрів узагальненим методом найменших квадратів. Вибирається те значення параметра l, яке дає змогу мінімізувати суму квадратів залишків
< 1. Це означає, що довільно вибирається параметр l, на основі якого формується матриця V з (24). Ця матриця в свою чергу дає змогу знайти оцінки параметрів узагальненим методом найменших квадратів. Вибирається те значення параметра l, яке дає змогу мінімізувати суму квадратів залишків  , а звідси і стандартну помилку параметрів. Тобто використовується поступовий перебір значень l на певному інтервалі, доки не буде знайдено той параметр, який забезпечує найкращий розв’язок.
, а звідси і стандартну помилку параметрів. Тобто використовується поступовий перебір значень l на певному інтервалі, доки не буде знайдено той параметр, який забезпечує найкращий розв’язок. ,
,  ;
; . (26)
. (26) . Отже,
. Отже, .
. ,
, .
. ,
, .
. :
: (27)
(27) ,
, 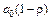 і a 2 плюс випадкове відхилення. Тоді ці параметри можна відшукати на основі 1МНК. Матриця вихідних даних
і a 2 плюс випадкове відхилення. Тоді ці параметри можна відшукати на основі 1МНК. Матриця вихідних даних 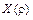 матиме вигляд:
матиме вигляд: .
. ,
, ,
,  відоме, то можна сформувати матрицю
відоме, то можна сформувати матрицю .
.

 . (28)
. (28)


