Алгоритм. Крок 1. Вибирається деяке початкове значення = , воно підставляється в рівняння (28), яке відповідно спрощується.
Крок 1. Вибирається деяке початкове значення Крок 2. Мінімізується сума квадратів залишків рівняння (28) при фіксованому Крок 3. Підставимо значення параметрів Крок 4. Задавши Процес продовжується доти, поки не буде досягнуто збіжності оцінок параметрів моделі на двох останніх кроках з вибраною точністю. Застосовується також процедура, що використовує інструментальні змінні, бо yt залежить від vt, а yt залежить від yt– 1. Одна зі складнощів моделі – це існування кореляції
можна знайти за допомогою 1МНК. Кількість лагових значень X, які включаються в цю модель, можна вибрати залежно від обсягу вибірки і від їх здатності пояснити поводження залежної змінної Алгоритм Уоліса. Уоліс запропонував складніший трикроковий метод оцінювання. Крок 1. Оцінюються параметри моделі
де
де Крок 2. Для залишків цієї моделі
де Крок 3. За допомогою оцінки, здобутої для r, формують матрицю:
і обчислюють оцінку вектора
Проведені Уолісом експерименти показали, що його метод оцінювання приводить до значно менших величин зміщення і до меншої суми квадратів залишків, ніж застосування методу Ейткена безпосередньо до моделі (16). Приклад. Необхідно побудувати економетричну модель, яка характеризує залежність між витратами на харчування і доходом сім’ї згідно з даними, що наведені в табл. 1.
Таблиця 1
Розв’язання 1. Ідентифікація змінних та специфікація моделі. yt – витрати на харчування в період t, залежна змінна; xt – дохід в період t, пояснююча змінна; yt– 1 – витрати на харчування в період t– 1, пояснювальна змінна. Економетрична модель має вигляд: yt = a 0 + a 1 xt + a 2 yt– 1 + ut ;
Таким чином, витрати на харчування в період t залежать від доходу в період t та від витрат на харчування в період t– 1. 2. Оцінка параметрів моделі. Для оцінювання параметрів цієї моделі застосуємо алгоритм Уолліса, який базується на методах інструментальних змінних і Ейткена. 2.1. Оцінка параметрів моделі виконується на основі методу інструментальних змінних, де Xt– 1 використовується як інструментальна змінна для Yt– 1. Отже, в операторі оцінювання
Економетрична модель має вигляд
2.2. Визначимо розрахункові значення Таблиця 2
Обчислимо критерій Дарбіна–Уотсона:
Для рівня значущості a = 0,05, n = 9, m = 3 критичні значення критерію Дарбіна–Уотсона дорівнюють: DW 1 = 0,629; DW 2 = 1,699. Звідси DW 1 < DW < DW 2, а це означає, що при даній сукупності спостережень важко зробити висновок про наявність чи відсутність автокореляції. Але, взявши до уваги, що значення DW дуже близьке до нижньої критичної межі критерію, ми не можемо відхилити гіпотезу про відсутність автокореляції. Ця величина критерію може свідчити про те, що залишки, які одержані на основі побудованої моделі, мають додатну автокореляцію. Визначимо коефіцієнт автокореляції:
2.3. Складемо матрицю S– 1.
2.4. Застосуємо оператор Ейткена для оцінювання параметрів моделі:
Економетрична модель: Yt = 1,1216 + 0,7944 Xt + 0,8733 Yt– 1. 3. Аналіз економетричної моделі. Розрахункові значення Таблиця 3
3.1. Залишкова дисперсія
3.2. Загальна дисперсія
3.3. Дисперсії та стандартні помилки оцінок параметрів моделі:
3.4. Коефіцієнти детермінації та кореляції:
R = 0,92. 3.5. Критерій Фішера (F -критерій)
F (0,05)крит = 4,46; F факт > F табл . Наведені щойно характеристики дисперсійного аналізу економетричної моделі свідчать про значущість зв’язку між витратами на харчування в період t і доходом в період t, а також витратами на харчування в період t – 1(F крит < F факт). Коефіцієнт детермінації показує, що на 85% варіація витрат на харчування визначається варіацією пояснювальних змінних моделі. Коефіцієнт кореляції також показує, що зв’язок є тісним. Оцінки параметрів моделі мають порівняно високі стандартні помилки, що свідчить про їх неефективність. Це пов’язано з варіацією фактичних спостережень змінної yt в часі та кількістю спостережень. Отже, при оцінці параметрів моделі, яка розглядалась в прикладі, були порушені дві необхідні умови для застосування методу 1МНК: 1) 2) Два етапи оцінювання параметрів економетричної моделі на основі алгоритму Уолліса спочатку враховують умову Контрольні запитання 1. Що таке лаг і що означає «лагова змінна»? 2. Дайте означення моделі розподіленого лагу. 3. Чим відрізняється модель розподіленого лагу від узагальненої моделі розподіленого лагу? 4. Яку схему розподіленого лагу запропонував Койк? 5. Назвіть найпростіші гіпотези, які застосовуються відносно залишків в моделях розподіленого лагу. 6. Як оцінюються параметри моделей при різних формах залишків? 7.Опишіть алгоритм ітеративного методу для оцінювання параметрів моделі. 8. Опишіть трикрокову процедуру оцінювання за Уоллісом.
|

 =
=  , воно підставляється в рівняння (28), яке відповідно спрощується.
, воно підставляється в рівняння (28), яке відповідно спрощується. ,
,  ,
,  .
.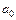 =
= 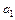 =
=  =
=  , тобто застосовується 1МНК до рівняння
, тобто застосовується 1МНК до рівняння  , що і дозволяє знайти
, що і дозволяє знайти  .
. ,
,  ,
,  .
. з
з  . Але, враховуючи зроблене припущення, коли пояснювальні змінні ймовірніше всього не корелюють з
. Але, враховуючи зроблене припущення, коли пояснювальні змінні ймовірніше всього не корелюють з 
 . Якщо значення змінної X має високу автокореляцію, то навряд чи потрібно брати більше ніж два її лагових значення. Записане вище співвідношення зрушимо на один період назад, щоб дістати
. Якщо значення змінної X має високу автокореляцію, то навряд чи потрібно брати більше ніж два її лагових значення. Записане вище співвідношення зрушимо на один період назад, щоб дістати 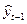 і підставимо вираз
і підставимо вираз 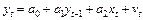 ,
, використовується як інструментальна змінна для
використовується як інструментальна змінна для  ,
, і
і  ,
,  .
. розраховують коефіцієнт автокореляції першого порядку з урахуванням поправки на зміщення:
розраховують коефіцієнт автокореляції першого порядку з урахуванням поправки на зміщення: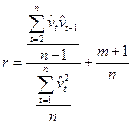 ,
, .
.
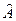 узагальненим методом найменших квадратів:
узагальненим методом найменших квадратів: .
. .
. матриці
матриці  та X запишуться так:
та X запишуться так: ;
;  .
.







 , відхилення їх від фактичних ut = Yt –
, відхилення їх від фактичних ut = Yt –  та дослідимо ці відхилення на наявність автокореляції (табл. 2).
та дослідимо ці відхилення на наявність автокореляції (табл. 2).

 .
. .
. ;
; .
. ;
;


 .
.
 )2
)2
 .
. .
. ;
; .
. ;
;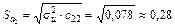 .
. ;
; ;
; ;
; .
. (застосовується метод інструментальних змінних), а потім
(застосовується метод інструментальних змінних), а потім 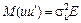 (застосовується метод Ейткена).
(застосовується метод Ейткена).


