Оцінювання очікуваного рівня продуктивності праці.
Оскільки прийняття рішень завжди пов’язане з оцінюванням прогнозного (очікуваного) значення, то дуже важливо визначити прогнозні якості моделі. Для цього з 20-ти спостережень вихідної інформації для побудови моделі продуктивності праці використано 17. Останні три спостереження використаємо, щоб оцінити якість прогнозу на основі моделі. Для останніх трьох спостережень підставимо значення чинників в отримані моделі продуктивності праці і знайдемо значення продуктивності праці. На основі лінійної моделі:
На основі степеневої моделі:
1. Визначимо відхилення між фактичними і розрахунковими значеннями продуктивності праці. Лінійна модель:
степенева модель:
2. Знайдемо похибки прогнозу. 1) середньоарифметична абсолютна похибка:
Лінійна модель: МАЕ = 0,94; степенева модель: МАЕ =1,34; б) середньоквадратична похибка прогнозу:
Лінійна модель: МSЕ = 1,17; степенева модель; МSЕ = 2,22; в) відносна похибка прогнозу:
лінійна модель: МАРЕ = 1,38%; степенева модель: МАРЕ = г) коефіцієнт невідповідності Тейла:
лінійна модель: Кт – 1,08 / (68,02 4 + 67,01) = 1,08/135,1 = 0,008; степенева модель: Кт – 1,49 / (68,02 + 68,60) = 1,49 / 136,62 = 0,011. Як свідчать похибки прогнозу, моделі продуктивності праці (лінійна і степенева) мають великі прогнозні можливості – абсолютні та відносні похибки незначні за рівнем і свідчать про добру апроксимацію моделі. Коефіцієнти невідповідності Тейла наближаються до нуля, що свідчить також про якісний прогноз. Порівнявши кожну з похибок для лінійної та степеневої моделі, можна помітити, що кожна з них має дещо нижчий рівень для лінійної моделі, але це не означає, що вона має істотні переваги перед степеневою, оскільки лінійна модель дає обернений зв’язок між стажем і продуктивністю праці, що суперечить теоретичним уявленням про цей зв’язок. 3. Визначимо прогноз продуктивності праці на наступні чотири місяці року, задавши очікуване значення чинників на цей період.
Визначимо відхилення очікуваного рівня продуктивності праці, отриманого на базі лінійної та степеневої моделей:
Як свідчать наведені відхилення, прогнозні рівні продуктивності праці, що їх здобуто на основі лінійної та степеневої моделей, різняться неістотно. Прогнозний рівень продуктивності праці може бути основою для прийняття рішень стосовно зміни цього показника на останній квартал року.
Наведений приклад виробничої функції показує, що ця економетрична модель дає змогу досить широко проаналізувати виробничу діяльність, визначити шляхи її вдосконалення з метою підвищення ефективності. Обґрунтованість такого аналізу повністю залежить від достовірності економетричної моделі, від того, наскільки вона адекватна реальному процесу. Проблема побудови виробничої функції або інших технологічних взаємозалежностей у виробництві – класична проблема економетрії. Контрольні запитання 1. Поняття про виробничу функцію Кобба-Дугласа, її загальний вигляд. 2. Гіпотези виробничої функції Кобба-Дугласа. 3.Який вигляд має система нормальних рівнянь для визначення параметрів виробничої функції? 4.Як інтепретуються параметри виробничої функції Кобба-Дугласа? 5.Як оцінити параметри функції на значущість? 6. Як перевірити побудовану виробничу функцію Кобба-Дугласа на адекватність?
Завдання. На основі вихідних даних табл. 2 – 4 виконати наведені далі завдання: 1. Побудувати модель продуктивності праці, яка характеризує залежність між рівнем продуктивності праці і чинниками, що впливають на нього (використати 20 спостережень). 2. Оцінити вірогідність моделі та оцінок її параметрів. 3. Визначити прогнозні властивості моделі продуктивності праці. 4. Знайти точковий та інтервальний прогнози продуктивності праці при заданих значеннях чинників на плановий період (останній квартал року). 5. Дати економіко-математичиий аналіз моделі. Показати, як можна використати характеристики взаємозв’язку в управлінні рівнем продуктивності праці.
Таблиця 2
Таблиця 3
Таблиця 4
|

 ,
,  ,
, .
. ,
,  ,
, .
.
 ;
;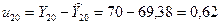 ;
; ;
; ;
; .
. .
. .
. ,
, ;
; ;
; ;
; ;
; .
.


