Метод Дарбіна
Цей метод базується на простій двокроковій процедурі. l Крок 1. Підставляємо значення залишків, яке задовольняє авторегресійну модель першого порядку
в економетричну модель
Тоді
де Звідси
У даному разі
За методом 1МНК обчислюємо оцінки параметрів l Крок 2. Застосовуємо оцінку параметра Прогноз згідно з економетричною моделлю, що має автокорельовані залишки, подається так:
Згідно з даними табл.1 теми 6 побудуємо економетричну модель продуктивності праці, якщо залишки, здобуті за 1 МНК, є автокорельованими. Для цього необхідно виконати такі завдання. 1. Дослідити залишки на наявність автокореляції. 2. Оцінити параметри моделі методом Ейткена та методом перетворення вихідної інформації. 3. Дослідити статистичну значущість моделі та оцінок її параметрів. 4. Визначити прогнозний рівень продуктивності праці. 5. Зробити порівняльний аналіз кількісних характеристик взаємозв’язку, здобутих методом 1 МНК і методом Ейткена. Розв’язування 1. Дослідимо залишки, здобуті згідно з 1 МНК, на наявність автокореляції, обчисливши: 1) критерій Дарбіна–Уотсона; 2) критерій фон Неймана; 3) циклічний коефіцієнт кореляції. 1) Знайдемо оцінку критерію Дарбіна–Уотсона:
Порівняємо значення критерію DW з табличними при α = 0,05 і n = 17. Критичні значення критерію DW у цьому разі такі: DW 1 = 0,48 – нижня межа; DW 2 = 1,85 – верхня межа. Оскільки DW факт > DW 2, то при α = 0,05 можна стверджувати що залишки ut не є автокорельованими. Наявність чи відсутність автокореляції залишків можна також визначити за критерієм фон Неймана. 2) Критерій фон Неймана 3) Визначимо циклічний коефіцієнт автокореляції:
Якщо значення цього коефіцієнта скоригувати на можливе зміщення, то циклічний коефіцієнт кореляції буде:
2. Скориставшись методом Ейткена, оцінимо параметри економетричної моделі з автокорельованими залишками. Оператор оцінювання запишеться так: або де
1) Формування матриці
де Запишемо матрицю
2) Оцінимо параметри моделі на основі оператора Ейткена:
Економетричну модель продуктивності праці подамо у вигляді: y = 50,869 + 0,404 x 1 – 1,672 x 2 – 2,479 x 3 – 0,048 x 4. (3) 3) Дослідимо статистичну значущість моделі та оцінок її параметрів. 1) коефіцієнт детермінації; 2) коефіцієнт кореляції; 3) F -критерій; 4) t -критерій. Коефіцієнт детермінації R 2 = 0,858. Він показує, що варіація продуктивності праці на 85,8% визначається досліджуваними чинниками. Коефіцієнт кореляції R = 0,926. На підставі цього коефіцієнта можна стверджувати, що зв’язок між продуктивністю праці та досліджуваними чинниками – фондомісткістю, коефіцієнтом плинності, рівнем втрат робочого часу і стажем – тісний. Критерій Фішера F = 18,16. Табличне його значення за рівня значущості α = 0,05, коли є m – 1 = 4, n – m = 12 ступенів свободи, дорівнює 5,78. Оскільки F факт > F табл, то гіпотеза про статистичну значущість зв’язку на основі економетричної моделі (3) підтверджується. Перевіримо достовірність кожної оцінки параметрів моделі, зокрема на основі t -критеріїв. Вони дорівнюють:
Табличне значення t -критерію для рівня значущості α = 0,05 та ступеня свободи n – m = 12 дорівнює 1,782. Оскільки 4) Подамо точковий та інтервальний прогнози продуктивності праці згідно з економетричною моделлю (3). Запишемо співвідношення, яке визначатиме прогнозний рівень продуктивності праці:
де Задамо очікувані значення досліджуваних чинників на наступні чотири місяці:
Підставивши послідовно компоненти кожного з векторів в економетричну модель
і додавши
Для визначення інтервального прогнозу продуктивності праці обчислимо спочатку стандартні похибки прогнозу для кожного періоду за формулою
а потім – граничні:
Додавши до точкового прогнозу продуктивності праці граничну похибку та віднявши її, дістанемо максимальний і мінімальний рівень її для кожного з періодів прогнозування:
Отже, як показують наведені дані, розмах варіації для кожного з періодів перебуває в межах 10 одиниць. Гранична похибка до прогнозного рівня продуктивності праці становить менш як 10%, а це свідчить про доволі високу якість прогнозування згідно з економетричною моделлю. 5) Виконаємо порівняльний аналіз характеристик взаємозв’язку, здобутих методом Ейткена. 6)
Порівнюючи оцінки параметрів моделі, здобутих за допомогою 1 МНК і методом Ейткена, доходимо висновку, що загальна тенденція впливу чинників на продуктивність праці не змінилася, але рівень оцінок став дещо іншим. Ці зміни є незначними. Деякі параметри збільшилися, деякі – зменшилися. Такі зміни зумовлені сутністю методу Ейткена, який уточнює параметри моделі за наявності навіть незначних взаємозв’язків залишків. Як бачимо з наведених даних, усі характеристики дисперсійного аналізу за методом Ейткена дещо нижчі, ніж за методом 1 МНК, оскільки метод Ейткена уточнює дисперсію залишків та дисперсії оцінок параметрів моделі, які в разі застосування 1 МНК завжди будуть нижчими від істинних, коли в моделі залишки автокорельовані. І нарешті, очікуваний рівень залежної змінної на основі економетричної моделі, побудованої за методом Ейткена, дещо вищий, ніж за методом 1 МНК. Це зумовлюється тим, що метод Ейткена вимагає включення системної складової залишків. Контрольні запитання 1. Дайте означення автoкореляції. 2. Які причини виникнення автокореляції залишків? 3. Як впливає автокореляція залишків на оцінку параметрів економетричної моделі? 4. Чим відрізняється метод оцінювання параметрів за методом Ейткена при автокореляції? 5. Запишіть матриці перетворення вихідної інформації згідно з двокроковою процедурою. 6. В яких випадках при автокореляції залишків доцільніше використовувати методи Кочрена – Оркатта або Дарбіна? 7. Дайте коротку характеристику алгоритму метода Кочрена – Оркатта. 8. Чим відрізняється метод Дарбіна від методу Кочрена – Оркатта? 9. Як записати формулу прогнозу залежної змінної при автокореляції залишків? Чому вона має такий вигляд? Завдання. Згідно з варіантами вихідних даних завдання до теми 6 виконати такі дії: 1) дослідити залишки на наявність автокореляції; 2) визначити матрицю 3) оцінити параметри економетричної моделі методом Ейткена; 4) обчислити матрицю коваріацій та стандартні похибки оцінок параметрів; 5) оцінити достовірність моделі та її параметрів; 6) визначити точковий та інтервальний прогнози залежної змінної; 7) виконати порівняльний аналіз економетричних моделей та кількісних характеристик взаємозв’язку, побудованих методом 1 МНК і методом Ейткена.
|


 .
.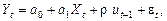
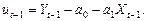

 має скалярну матрицю дисперсій:
має скалярну матрицю дисперсій:
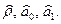
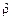 для перетворення змінних
для перетворення змінних 
 і
і  , а метод 1 МНК – для перетворених даних.
, а метод 1 МНК – для перетворених даних.
 .
.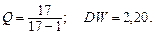 Це значення порівнюється з табличним
Це значення порівнюється з табличним  при n = 17 і α = 0,05. Оскільки
при n = 17 і α = 0,05. Оскільки 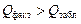 , то автокореляція відсутня.
, то автокореляція відсутня. .
. .
.
 – матриця, обернена до матриці S;
– матриця, обернена до матриці S; – матриця, обернена до матриці V.
– матриця, обернена до матриці V. .
. ,
, .
. для вихідних даних:
для вихідних даних:





 .
. .
.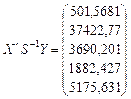 ;
;  .
. ;
;  ;
;  ;
;  ;
; 
 ;
; ;
;  .
. ;
;  ;
; ;
;  ;
; .
. ,
,  і
і 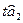 перевищують ці значення, то відповідні параметри моделі є достовірними, а
перевищують ці значення, то відповідні параметри моделі є достовірними, а  і
і  менші за критичне значення. Звідси
менші за критичне значення. Звідси  ,
, – вектор очікуваних значень досліджуваних чинників (пояснюючих змінних);
– вектор очікуваних значень досліджуваних чинників (пояснюючих змінних);  – коефіцієнт коваріації залишків;
– коефіцієнт коваріації залишків;  – залишки залежної змінної, здобуті за допомогою 1 МНК, для останнього спостереження матриці вихідних даних
– залишки залежної змінної, здобуті за допомогою 1 МНК, для останнього спостереження матриці вихідних даних  .
. ;
; ;
; ;
; .
.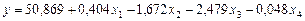
 , дістанемо прогнозні значення продуктивності праці:
, дістанемо прогнозні значення продуктивності праці: ;
;  ;
;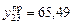 ;
;  .
. ;
;  ,
, ;
;  .
. ;
;  ;
; ;
;  .
. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
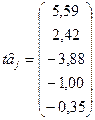 ;
;
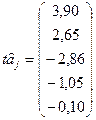 ;
;
 ;
;
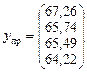 .
.
 ;
;


