WritingWrite a composition on “The greatest mathematicians of antiquity”. Extended reading Text C. Solution of Polynomial Equations of Third and Higher Degree
Read and translate the text into Ukrainian at home. Give some more details and your own comments concerning all the algebraists mentioned in the text. Write a summary and express the main ideas of the text. Reproduce it in class. The first records of man's interest in cubic equations date from the time of the old Babylonian civilization, about 1800-1600 B.C. Among the math materials that survive, are tables of cubes and cube roots, as well as tables of values of In the Greek period concern with volumes of geometrical solids led easily to problems that in modern form involve cubic equations. The well-known problem of duplicating the cube is essentially one of solving the equation The well-known Persian poet and mathematician Omar Khayyám (1100 A.D.) advanced the study of the cubic by essentially Greek methods. He found solutions through the use of conies. It is typical of the state of algebra in his day that he distinguished thirteen special types of cubics that have positive roots. For example, he solved equations of the type The next major advance was the algebraic solution of the cubic. This discovery, a product of the Italian Renaissance, is surrounded by an atmosphere of mystery; the story is still not entirely clear. The method appeared in print in 1545 in the Ars Magna of Girolamo Cardano of Milan, a physician, astrologer, mathematician, prolific writer, and suspected heretic, altogether one of the most colourful figures of his time. The method gained currency as "Cardan's formula" (Cardan is the English form of his name). According to Cardano himself, however, the credit is due to Scipione del Ferro, a professor of maths at the University of Bologna, who in 1515 discovered how to solve cubics of the type In 1535 Fior challenged the prominent mathematician Niccolo Tartaglia of Brescia (then teaching in Venice) to a contest because Fior did not believe Tartaglia's claim of having found a solution for cubics of the type Although couched in geometrical language the method itself is algebraic and the style syncopated. Cardano gives as an example the equation
The procedure easily applies to the general cubic after being transformed to remove the term in
for the real root, The general quartic equation yielded to methods of similar character; and its solution, also, appeared in Ars Magna. Cardano's pupil Ludovico Ferrari was responsible for this result. Ferrari, while still in his teens (1540), solved a challenging problem that his teacher could not solve. His solution can be described as follows: First reduce the general quartic to one in which the Later efforts to solve the quintic and other equations were foredoomed to failure, but not until the nineteenth century was this finally recognized. Karl Friedrich Gauss proved in 1799 that every algebraic equation of degree n over the real field has a root (and hence n roots) in the complex field. The problem was to express these roots in terms of the coefficients by radicals. Paolo Ruffini, an Italian teacher of maths and medicine at Modena, gave (in 1813) an essentially satisfactory proof of the impossibility of doing this for equations of degree higher than four, but this proof was not well-known at the time and produced practically no effect.
|
. Such tables could have been used to solve cubics of special types. For example, to solve the equation 
, the Babylonians might have first multiplied by 4 and made the substitution 
, giving 
. Letting 
,this becomes 
. From the tables, onesolution is 
, and hence 6 is a root of the original equation.
. This problem, impossible of solution by ruler and compasses alone, was solved in an ingenious manner by Archytas of Tarentum (c. 400 B.C.), using the intersections of a cone, a cylinder, and a degenerate torus (obtained by revolving a circle about its tangent).
(where b and с are positive numbers) by finding intersections of the parabola 
and the circle 
, where the circle is tangent to the axis of the parabola at its vertex. The positive root of Omar Khayyám's equation is represented by the distance from the axis of the parabola to a point of intersection of the curves.
.As was customary among mathematicians of that time, he kept his methods secret in order to use them for personal advantage in math duels and tournaments. When he died in 1526, the only persons familiar with his work were a son-in-law and one of his students, Antonio Maria Fior of Venice.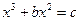
. A few days before the contest Tartaglia managed to discover also how to solve cubics of the type 
, a discovery (so he relates) that came to him in a flash during the night of February 12/13, 1535. Needless to say, since Tartaglia could solve two types of cubics whereas Fior could solve only one type, Tartaglia won the contest. Cardano, hearing of Tartaglia's victory, was eager to learn his method. Tartaglia kept putting him off, however, and it was not until four years later that a meeting was arranged between them. At this meeting Tartaglia divulged his methods, swearing Cardano tо secrecy and particularly forbidding him to publish it. This oath must have been galling to Cardano. On a visit to Bologna several years later he met Ferro's son-in-law and learned of Ferro's prior solution. Feeling, perhaps, that this knowledge released him from his oath to Tartaglia, Cardano published a version of the method in Ars Magna. This action evoked bitter attack from Tartaglia, who claimed that he had been betrayed.
and seeks two unknown quantities, p and q, whose difference is the constant term 20 and whose product is the cube of 1/3 the coefficient of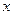 
, 8. A solution is then furnished by the difference of the cube roots of p and q. For this example the solution is
.
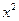. This discovery left unanswered such questions as these: What should be done with negative and imaginary roots, and (a related question) do three roots always exist? What should be done (in the so-called irreducible case) when Cardano's method produced apparently imaginary expression like
, of the cubic 
? These questions were not fully settled until 1732, when Leonard Euler found a solution.
term is missing, then rearrange the terms and add a suitable quantity (with undetermined coefficient) to both sides so that the left-hand member is a perfect square. The undetermined coefficients are then determined so that the right-hand member is also a square, by requiring that its determinant be zero. This condition leads to a cubic, which can now be solved – the quartic can then be easily handled.
