Чистый изгиб
Чистый изгиб будет иметь место, если к горизонтально расположенному стержню подвесить на одинаковом расстоянии от опор два одинаковых груза, как показано на рисунке 4.4. a) При такой деформации продольные волокна стержня будут искривляться по дуге окружности, поперечные сечения, плоские до деформации, останутся плоскими и перпендикулярными оси после деформации, но повернутся на некоторый угол j. Длина осевых (нейтральных) волокон не изменится, нижние волокна удлинятся, а верхние укоротятся (рис.4.4). Как и при осевом растяжении, будут только продольные деформации связей. Если, учитывая гипотезу о малости перемещений, закон изменения деформаций по высоте сечения считать линейным, то относительное удлинение каждой связи будет зависеть от расстояния между нейтральным волокном и этой связью y и от изменения кривизны стержня в рассматриваемом сечении k = j / l Таким образом, ez = Dl/ l =k×y, ex = ey = 0, gxy = gxz = gzy = 0 .
Если разделить стержень любым произвольным сечением на две части и заменить разорванные связи усилиями в них (напряжениями) (рис.4.4, г), то на основании соотношения (3.10) sz=E×ez= E×k×y, sx = sy = txy = txz = tzy. (4.2) Нормальные напряжения s приводятся к паре сил с моментом (4.3) который называется изгибаим моменто относительно оси x. Подставля оотношения (4.2) в (4.3), получим
Mx = E×k×Ix. (4.4) Знак момента определяется знаком координаты y и напряжения sz и совпадает со знаком кривизны. Из соотношения (4.2): k = sz / (E×y). Подставляя это выражение в (4.4), получим формулу, связывающую изгибающий момент с напряжениями в связях Mx = sz×I / y. (4.5) Геометрические характеристики часто встречающихся сечений приведены в таблице 4.1, а прокатных профилей - в таблицах
|
.
.
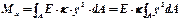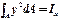представляет собой геометрическую характеристику сечения стержня и называется моментом инерции сечения относительно оси x. С учетом этого обозначения будем иметь
