Рассмотрим два сообщающихся сосуда, наполненных различными, не смачивающимися между собой жидкостями (рис. 2.6).
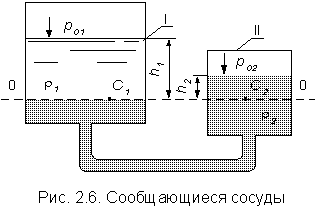 Сосуды закрыты, давления
Сосуды закрыты, давления  и
и  – на поверхности жидкостей в сосудах I и II различны. Линия О-О – линия раздела разнородных жидкостей. Горизонтальная плоскость, проходящая через линию О-О, является плоскостью равного давления. Определим величину гидростатического давления в точках
– на поверхности жидкостей в сосудах I и II различны. Линия О-О – линия раздела разнородных жидкостей. Горизонтальная плоскость, проходящая через линию О-О, является плоскостью равного давления. Определим величину гидростатического давления в точках  и
и  , лежащих на плоскости равного давления. Согласно основному уравнению гидростатики:
, лежащих на плоскости равного давления. Согласно основному уравнению гидростатики:
 (2.30)
(2.30)
 (2.31)
(2.31)
где  и
и  – возвышение поверхности жидкостей в сосудах I и II над плоскостью О-О;
– возвышение поверхности жидкостей в сосудах I и II над плоскостью О-О;  и
и 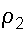 – плотности жидкостей.
– плотности жидкостей.
Очевидно, что:

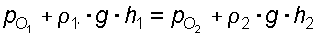 (2.32)
(2.32)
 (2.33)
(2.33)
Зависимость (2.33) характеризует условия равновесия жидкостей в сообщающихся сосудах. Она позволяет решать частные задачи.
Случай I. В сосудах налита одинаковая жидкость, но давления  и
и  различны.
различны.
тогда при условии, что 
 получим:
получим:
 (2.34)
(2.34)
Случай II. Жидкость одинакова, т.е.  и
и  . Тогда:
. Тогда:
 (2.35)
(2.35)
жидкость в сосудах будет на одном уровне.
Случай III. Жидкость одинакова  , но один сосуд открыт
, но один сосуд открыт  , а другой закрыт
, а другой закрыт  .Тогда:
.Тогда:
 (2.36)
(2.36)
 (2.37)
(2.37)
так как  , значит
, значит
 (2.38)
(2.38)
 (2.39)
(2.39)
Выражение  есть пьезометрическая высота для точек, лежащих на поверхности жидкости в закрытом сосуде.
есть пьезометрическая высота для точек, лежащих на поверхности жидкости в закрытом сосуде.
Случай IV. Жидкости разнородные, несмешивающиеся, а  Тогда:
Тогда:

 (2.40)
(2.40)
или
 (2.41)
(2.41)
Рассмотрим закрытый сосуд с жидкостью, к которому в точках А и В на произвольной глубине  присоединены пьезометры I и II (рис. 2.7).
присоединены пьезометры I и II (рис. 2.7).
 Давление на свободной поверхности в сосуде
Давление на свободной поверхности в сосуде  больше атмосферного
больше атмосферного  . Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному
. Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному  . Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю
. Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю  .
.
Для определения вертикальных координат точек А и В проведем на произвольной высоте горизонтальную плоскость 0-0. Эта плоскость называется плоскостью сравнения. Вертикальное расстояние от плоскости сравнения до рассматриваемой точки называется геометрической высотой точки по отношению к плоскости сравнения и обозначается буквой  . За плоскость сравнения может быть принят уровень земли, пола.
. За плоскость сравнения может быть принят уровень земли, пола.
Так как давление в сосуде на свободной поверхности жидкости больше атмосферного, то в пьезометрических трубках I и II жидкость поднимется на большую высоту, чем уровень жидкости в сосуде. Обозначим высоту поднятия жидкости в открытом пьезометре через
 – пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через
– пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через  – приведенная высота.
– приведенная высота.
Пьезометрическая высота  – мера манометрического давления в точке А. Приведенная высота
– мера манометрического давления в точке А. Приведенная высота  – мера абсолютного давления в точке В. Разность высот
– мера абсолютного давления в точке В. Разность высот  , равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст.
, равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст.
Сумма геометрической высоты  и пьезометрической
и пьезометрической  для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором:
для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором:
 . (2.42)
. (2.42)
Но
 . (2.43)
. (2.43)
Подставив это выражение в формулу (2.42) получим
 (2..44)
(2..44)
или
 (2.45)
(2.45)
 это сумма приведенной высоты и геометрической высоты положения, называемая гидростатическим напором
это сумма приведенной высоты и геометрической высоты положения, называемая гидростатическим напором  .
.
Тогда:
 (2.46)
(2.46)
 В уравнении (2.46)
В уравнении (2.46)  для любой точки жидкости, а
для любой точки жидкости, а  не зависит от положения точки.
не зависит от положения точки.
Значит:

 (2.47)
(2.47)
Поэтому, сколько бы мы пьезометров не подключили, во всех пьезометрах жидкость установится на одном уровне: плоскость, соответствующая уровню П–П, называется пьезометрической плоскостью, а уровню Н–Н – напорной плоскостью.
Пьезометрический напор является мерой удельной потенциальной энергии жидкости. Предположим, что вес частицы жидкости в точке А. равен  (рис. 2.7). По отношении к плоскости сравнения О – О запас потенциальной энергии положения равен
(рис. 2.7). По отношении к плоскости сравнения О – О запас потенциальной энергии положения равен  , где
, где  -.высота от плоскости О – О до точки А. Под действием избыточного гидростатического давления
-.высота от плоскости О – О до точки А. Под действием избыточного гидростатического давления  частица, находящаяся на глубине
частица, находящаяся на глубине  , может подняться на высоту
, может подняться на высоту  ,то есть она обладает потенциальной энергией давления равной
,то есть она обладает потенциальной энергией давления равной  . Полная потенциальная энергия частицы жидкости весом
. Полная потенциальная энергия частицы жидкости весом  равна
равна  .Удельная потенциальная энергия, т.е. энергия приходящаяся на единицу веса частицы будет соответственно равна:
.Удельная потенциальная энергия, т.е. энергия приходящаяся на единицу веса частицы будет соответственно равна:
 (2.48)
(2.48)
Аналогично, гидростатический напор  является также мерой удельной потенциальной энергии жидкости, но большей по сравнению
является также мерой удельной потенциальной энергии жидкости, но большей по сравнению  на величину удельной потенциальной энергии атмосферного давления.
на величину удельной потенциальной энергии атмосферного давления.
 (2.49)
(2.49)

 Сосуды закрыты, давления
Сосуды закрыты, давления  и
и  – на поверхности жидкостей в сосудах I и II различны. Линия О-О – линия раздела разнородных жидкостей. Горизонтальная плоскость, проходящая через линию О-О, является плоскостью равного давления. Определим величину гидростатического давления в точках
– на поверхности жидкостей в сосудах I и II различны. Линия О-О – линия раздела разнородных жидкостей. Горизонтальная плоскость, проходящая через линию О-О, является плоскостью равного давления. Определим величину гидростатического давления в точках  и
и  , лежащих на плоскости равного давления. Согласно основному уравнению гидростатики:
, лежащих на плоскости равного давления. Согласно основному уравнению гидростатики: (2.30)
(2.30) (2.31)
(2.31) и
и  – возвышение поверхности жидкостей в сосудах I и II над плоскостью О-О;
– возвышение поверхности жидкостей в сосудах I и II над плоскостью О-О;  и
и 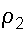 – плотности жидкостей.
– плотности жидкостей.
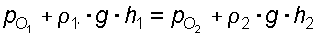 (2.32)
(2.32) (2.33)
(2.33) и
и  различны.
различны.
 получим:
получим: (2.34)
(2.34) и
и  . Тогда:
. Тогда: (2.35)
(2.35) , но один сосуд открыт
, но один сосуд открыт  , а другой закрыт
, а другой закрыт  .Тогда:
.Тогда: (2.36)
(2.36) (2.37)
(2.37) (2.38)
(2.38) (2.39)
(2.39) есть пьезометрическая высота для точек, лежащих на поверхности жидкости в закрытом сосуде.
есть пьезометрическая высота для точек, лежащих на поверхности жидкости в закрытом сосуде. Тогда:
Тогда:
 (2.40)
(2.40) (2.41)
(2.41) присоединены пьезометры I и II (рис. 2.7).
присоединены пьезометры I и II (рис. 2.7). Давление на свободной поверхности в сосуде
Давление на свободной поверхности в сосуде  больше атмосферного
больше атмосферного  . Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному
. Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному  . Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю
. Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю  .
. . За плоскость сравнения может быть принят уровень земли, пола.
. За плоскость сравнения может быть принят уровень земли, пола. – пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через
– пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через  – приведенная высота.
– приведенная высота. – мера манометрического давления в точке А. Приведенная высота
– мера манометрического давления в точке А. Приведенная высота  – мера абсолютного давления в точке В. Разность высот
– мера абсолютного давления в точке В. Разность высот  , равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст.
, равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст. для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором:
для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором: . (2.42)
. (2.42) . (2.43)
. (2.43) (2..44)
(2..44) (2.45)
(2.45) это сумма приведенной высоты и геометрической высоты положения, называемая гидростатическим напором
это сумма приведенной высоты и геометрической высоты положения, называемая гидростатическим напором  .
. (2.46)
(2.46) В уравнении (2.46)
В уравнении (2.46)  для любой точки жидкости, а
для любой точки жидкости, а  не зависит от положения точки.
не зависит от положения точки.
 (2.47)
(2.47) (рис. 2.7). По отношении к плоскости сравнения О – О запас потенциальной энергии положения равен
(рис. 2.7). По отношении к плоскости сравнения О – О запас потенциальной энергии положения равен  , где
, где  частица, находящаяся на глубине
частица, находящаяся на глубине  , может подняться на высоту
, может подняться на высоту  . Полная потенциальная энергия частицы жидкости весом
. Полная потенциальная энергия частицы жидкости весом  .Удельная потенциальная энергия, т.е. энергия приходящаяся на единицу веса частицы будет соответственно равна:
.Удельная потенциальная энергия, т.е. энергия приходящаяся на единицу веса частицы будет соответственно равна: (2.48)
(2.48) является также мерой удельной потенциальной энергии жидкости, но большей по сравнению
является также мерой удельной потенциальной энергии жидкости, но большей по сравнению  на величину удельной потенциальной энергии атмосферного давления.
на величину удельной потенциальной энергии атмосферного давления. (2.49)
(2.49)


