Оценки точности уравнения регрессии и его параметров
Стандартная ошибка оценки по регрессии. Как было отмечено, несмещённая оценка дисперсии остатков уравнения регрессии называется остаточной дисперсией
Корень квадратный из остаточной дисперсии называется стандартной ошибкой оценки по регрессии. Обозначается она обычно Sy,x и вычисляется по формуле Sy,x = Стандартная ошибка оценки по регрессии показывает, насколько в среднем мы ошибаемся, оценивая значение зависимой переменной по найденному уравнению регрессии при фиксированном значении независимой переменной. Оценка значимости уравнения регрессии (дисперсионный анализ регрессии). Для оценки значимости уравнения регрессии устанавливают, соответствует ли выбранная модель анализируемым данным. Для этого используется дисперсионный анализ регрессии. Основная его посылка – это разложение общей суммы квадратов отклонений
если в уравнении регрессии присутствует свободный член. В противном случае в правую часть надо добавить слагаемое 2 Второе слагаемое в правой части этого разложения уже встречалось и обсуждалось – это часть общей суммы квадратов отклонений, объясняемая действием случайных и неучтенных факторов. Первое слагаемое этого разложения – это часть общей суммы квадратов отклонений, объясняемая регрессионной зависимостью. Следовательно, если регрессионная зависимость между у и х отсутствует, то общая сумма квадратов отклонений объясняется действием только случайных факторов или ошибок, т.е. Будучи отнесёнными к соответствующему числу степеней свободы эти суммы называются средними квадратами отклонений и служат оценками дисперсии F = MSR/ MSE. Таким образом, F-статистика проверяет гипотезу о незначимости уравнения регрессии (H0: Расчётное значение F-статистики сравнивается с критическим значением (в нашем случае число степеней свободы числителя равно 1 (число регрессоров), а число степеней свободы знаменателя равно (n – 2)) с уровнем значимости При компьютерных расчётах в некоторых статистических пакетах программ оценка значимости уравнения регрессии осуществляется на основе дисперсионного анализа в таблицах вида:
Таблица 1.1 – Дисперсионный анализ регрессии
Здесь p-value – это вероятность выполнения неравенства F В некоторых статистических пакетах программ значение F-статистики и вероятность для неё приводятся без показа процедуры их вычисления. Если в уравнении регрессии нет константы, то в некоторых статистических пакетах F-статистика просто не вычисляется. Интервальные оценки параметров уравнения регрессии. При использовании параметров уравнения регрессии в анализе и прогнозировании для них необходимо уметь строить интервальные оценки. Доверительный интервал для коэффициента регрессии определяется из соотношения (b Sb= Доверительный интервал для свободного члена уравнения регрессии определяется из соотношения (а Sа= Интервальная оценка расчетных значений
Интервальная оценка прогнозных значений определяется из подобного же соотношения, только в стандартную ошибку добавляется ещё стандартное отклонение Проверка значимости параметров уравнения регрессии. Кроме проверки значимости уравнения регрессии в целом необходимо уметь проверять значимость каждого параметра уравнения регрессии в отдельности. Осуществляется это на основе t-статистик. Значения этих статистик рассчитываются из соотношений: ta = a /Sa, tb = b /Sb. Для этих статистик определяются критические значения или расчётные уровни значимости, на основе которых и принимаются решения о значимости или незначимости соответствующих параметров. В случае парной линейной регрессии проверка значимости уравнения регрессии в целом и проверка значимости коэффициента уравнения регрессии по сути дела одно и то же, т. к. в том и другом случае проверяется одна и та же гипотеза о том, что коэффициент уравнения регрессии равен нулю. Кроме того, можно показать, что для парной линейной регрессии F = Уравнение простой регрессии в компьютерных расчётах обычно выдаётся в виде следующей таблицы. Таблица 1.2 – Уравнение простой регрессии
Пересечение и наклон – это другое название свободного члена уравнения регрессии и его коэффициента, основанное на геометрическом смысле этих величин, если рассматривать уравнение регрессии как уравнение прямой линии или линии регрессии. Смысл остальных столбцов понятен из их названия. Кроме уже рассмотренных показателей точности уравнения регрессии обычно ещё используют коэффициент детерминации. Коэффициент детерминации (R- квадрат) является удобной оценкой качества подгонки данных моделью. Выясним его смысл. В общем случае коэффициент детерминации определяется из соотношения R2 = т. е. это доля выборочной дисперсии переменной y, которая объясняется моделью. Следует иметь в виду, что Известно, что если модель содержит свободный член, то справедливо соотношение (следует из
Отсюда следует, что Если уравнение регрессии содержит свободный член, то оба выражения для Можно показать, что в случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции, т.е. R2 = Следует иметь в виду, что
|

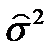 =
=  =
=  .
. .
. на составляющие. Известно, что такое разложение имеет вид
на составляющие. Известно, что такое разложение имеет вид +
+  ,
,
 . Но как было показано, второй член этого слагаемого (
. Но как было показано, второй член этого слагаемого (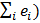 равен нулю, если в уравнении регрессии присутствует свободный член.
равен нулю, если в уравнении регрессии присутствует свободный член.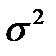 в разных предположениях. Одна из них рассчитывается в предположении отсутствия регрессионной зависимости, а другая – без такого предположения. Следовательно, если регрессионная зависимость отсутствует, то эти оценки должны быть близкими. Сравниваются они на основе F-отношения:
в разных предположениях. Одна из них рассчитывается в предположении отсутствия регрессионной зависимости, а другая – без такого предположения. Следовательно, если регрессионная зависимость отсутствует, то эти оценки должны быть близкими. Сравниваются они на основе F-отношения: = 0), т. е. о том, что зависимости между анализируемыми переменными нет. Если верна нулевая гипотеза, то F-статистика следует распределению Фишера и, зная уровень значимости и число степеней свободы числителя и знаменателя, можно определить критические значения этого распределения.
= 0), т. е. о том, что зависимости между анализируемыми переменными нет. Если верна нулевая гипотеза, то F-статистика следует распределению Фишера и, зная уровень значимости и число степеней свободы числителя и знаменателя, можно определить критические значения этого распределения. . Если F
. Если F  < F, то гипотеза о незначимости уравнения регрессии не отклоняется, т. е. не отклоняется гипотеза о том, что
< F, то гипотеза о незначимости уравнения регрессии не отклоняется, т. е. не отклоняется гипотеза о том, что 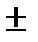 t
t  Sb), где Sb – стандартная ошибка оценки коэффициента регрессии. Известно, что
Sb), где Sb – стандартная ошибка оценки коэффициента регрессии. Известно, что .
. .
.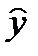 определяется доверительным интервалом (
определяется доверительным интервалом ( ), где
), где  стандартная ошибка оценки
стандартная ошибка оценки  , определяемая из соотношения
, определяемая из соотношения =
=  .
. , характеризующее рассеяние прогнозных значений зависимой переменной вокруг линии регрессии.
, характеризующее рассеяние прогнозных значений зависимой переменной вокруг линии регрессии. .
. ,
, также соответствует выборочному среднему
также соответствует выборочному среднему 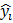 (см. соотношение (1.2)). Следовательно, коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленную вариацией независимой переменной. Обычно он выражается в процентах, поэтому, например, если R2 = 75%, то это значит, что 75% вариации зависимой переменной у объясняется вариацией независимой переменной х, а остальные 25% изменения у объясняются либо ошибками наблюдений, либо действием неучтенных факторов, либо тем и другим.
(см. соотношение (1.2)). Следовательно, коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленную вариацией независимой переменной. Обычно он выражается в процентах, поэтому, например, если R2 = 75%, то это значит, что 75% вариации зависимой переменной у объясняется вариацией независимой переменной х, а остальные 25% изменения у объясняются либо ошибками наблюдений, либо действием неучтенных факторов, либо тем и другим. )
)  (
( ) =
) =  ), откуда следует, что
), откуда следует, что = 1 –
= 1 –  = 1 –
= 1 –  .
. действительно определяет, какую долю выборочной вариации
действительно определяет, какую долю выборочной вариации 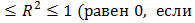 все
все  .
.


