Анализ матрицы парных коэффициентов корреляции
Такая матрица состоит из коэффициентов парных корреляций, рассчитанных для набора переменных y, x1, x2,….., xm и размещённых в виде матрицы. В дальнейшем переменную y будем называть зависимой, а остальные – независимыми. Для корреляционного анализа эти переменные равноправны, но для удобства анализа мы их будем различать. Поскольку rxy = ryx, то корреляционная матрица симметрична относительно главной диагонали, поэтому естественно анализировать только одну из её частей (верхнюю или нижнюю относительно главной диагонали). Пусть корреляционная матрица R имеет вид: y x1 x2 … xm
Задача анализа такой матрицы обычно преследует две цели – выявление значимых и мультиколлинеарных независимых переменных. Первая строка матрицы содержит коэффициенты корреляции между зависимой (y) и независимыми переменными (х1, х2, …, xm). Коэффициенты этой строки анализируются с целью выявления значимых независимых переменных. Значимость независимой переменной здесь понимается с точки зрения влияния её на зависимую переменную. Если проверка гипотезы Н0: Второй этап анализа матрицы парных коэффициентов корреляции заключается в выявлении мультиколлинеарности среди независимых переменных. Идеальным условием реализации регрессионного анализа является независимость между собой независимых переменных. Но это практически никогда не выполняется, и уж совсем нежелательно, чтобы между независимыми переменными наблюдалась тесная корреляционная взаимосвязь. В этом случае говорят о коллинеарности переменных. Считается, что две случайные переменные коллинеарные, если коэффициент корреляции между ними не менее 0,7. Если таких переменных несколько, то говорят о мультиколлинеарности. Мультиколлинеарность для регрессионного анализа нежелательна, и, как было отмечено, её выявление является одной из задач анализа матрицы парных коэффициентов корреляции. Для этого просматривается оставшаяся часть матрицы R (кроме первой строки) и выделяются коэффициенты, по величине ³ 0,7. Они и укажут на коллинеарные переменные. Обычно в уравнении регрессии оставляют те из значимых коллинеарных переменных, которые слабее связаны с другими зависимыми переменными.
|

 .
.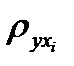 = 0 покажет, что эта гипотеза не отклоняется, то это означает, что соответствующая независимая переменная незначимо влияет на зависимую переменную, т. е. незначима, и в уравнение регрессии включать её не рекомендуется. Отметим, что подобные выводы предварительные и правомерны лишь на начальном этапе анализа информации, на самом деле взаимосвязи здесь более сложные, о чём речь ниже.
= 0 покажет, что эта гипотеза не отклоняется, то это означает, что соответствующая независимая переменная незначимо влияет на зависимую переменную, т. е. незначима, и в уравнение регрессии включать её не рекомендуется. Отметим, что подобные выводы предварительные и правомерны лишь на начальном этапе анализа информации, на самом деле взаимосвязи здесь более сложные, о чём речь ниже.


