Метод наименьших квадратов и его предпосылки
Рассмотрим уравнение линейной множественной регрессии. Уравнение генеральной совокупности или модель регрессии запишем в виде
где
Предполагается, что εt независимы и нормально распределены с нулевым математическим ожиданием и постоянной дисперсией Термины «зависимая» и «независимые» для переменных не совсем удачны и означают лишь, что в этом случае значения зависимой переменной оцениваются на основе известных значений независимых переменных. Приведём предпосылки спецификации классической регрессионной модели:
Кроме предпосылок спецификации модели необходимо выполнение ещё и предпосылок метода наименьших квадратов (МНК). Как известно, оценки параметров модели линейной регрессии обычно рассчитываются на основе МНК. Доказано, что эти оценки будут «хорошими», т.е. несмещёнными, эффективными и состоятельными, если будут выполняться следующие предпосылки относительно поведения остаточного члена
Кроме основных предпосылок, рассматриваются ещё две дополнительные – отсутствие между регрессорами сильной линейной зависимости (совершенной мультиколлинеарности) и что Одна из задач эконометрики – тестирование выполнимости предпосылок и выработка методов оценивания при их нарушениях. Оцененное уравнение регрессии будем записывать так:
Здесь Представим уравнение генеральной совокупности и оценённое уравнение регрессии в матричной форме. Введём следующие обозначения: Y = Тогда уравнения регрессии (2.1) и (2.2) в матричной форме примут вид Y = X МНК-оценки параметров уравнения (2.1) рассчитываются из условия минимизации по b квадратичной формы: Q(b) = Продифференцируем Q(b) по b и приравняем результат к нулю:
Откуда имеем b = Это и есть МНК-оценка параметров уравнения (2.1). Кроме того, известно, что несмещённая оценка дисперсии случайного члена
где
|

 , (t =
, (t =  ), (2.1)
), (2.1)
 – значения зависимой переменной с номером t;
– значения зависимой переменной с номером t; – значения независимых переменных с номером t;
– значения независимых переменных с номером t; – параметры уравнения регрессии,
– параметры уравнения регрессии,  – константа или свободный член уравнения регрессии,
– константа или свободный член уравнения регрессии,  – коэффициенты уравнения регрессии;
– коэффициенты уравнения регрессии; – значения случайного члена уравнения регрессии.
– значения случайного члена уравнения регрессии. , т. е.
, т. е.  N(0,
N(0,  эндогенная, зависимая переменная объясняется m экзогенными, независимыми переменными;
эндогенная, зависимая переменная объясняется m экзогенными, независимыми переменными; в общем случае уравнение регрессии включает константу;
в общем случае уравнение регрессии включает константу; объём выборки n должен быть значительно больше числа объясняющих переменных m (считается, что каждый регрессор должен быть обеспечен не менее 6–7 наблюдениями);
объём выборки n должен быть значительно больше числа объясняющих переменных m (считается, что каждый регрессор должен быть обеспечен не менее 6–7 наблюдениями); разность n–m–1 называется числом степеней свободы модели; чем она больше, тем надёжнее результаты оценивания;
разность n–m–1 называется числом степеней свободы модели; чем она больше, тем надёжнее результаты оценивания; параметры уравнения регрессии
параметры уравнения регрессии  должны быть постоянными для всей выборки; это положение зачастую определяет выборку.
должны быть постоянными для всей выборки; это положение зачастую определяет выборку. математическое ожидание
математическое ожидание  t;
t; дисперсия
дисперсия  t, в этом случае говорят, что в остатках наблюдается гомоскедастичность; в противном случае – гетероскедастичность;
t, в этом случае говорят, что в остатках наблюдается гомоскедастичность; в противном случае – гетероскедастичность; случайные отклонения
случайные отклонения  независимы друг от друга для t
независимы друг от друга для t  s, в этом случае говорят, что в остатках отсутствует какая-либо автокорреляция;
s, в этом случае говорят, что в остатках отсутствует какая-либо автокорреляция; регрессоры и остатки должны быть независимыми.
регрессоры и остатки должны быть независимыми. , (t =
, (t =  ). (2.2)
). (2.2) – оценки параметров уравнения регрессии, а
– оценки параметров уравнения регрессии, а  – выборочная реализация случайного процесса
– выборочная реализация случайного процесса 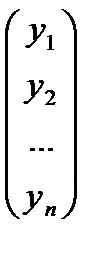 , X =
, X =  , b =
, b =  , e =
, e =  , и т. д.
, и т. д.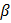 +
+ 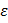 и Y = Xb + e. (2.3)
и Y = Xb + e. (2.3) e = (Y – Xb)T(Y – Xb) = YTY – 2YTXb – bTXTXb.
e = (Y – Xb)T(Y – Xb) = YTY – 2YTXb – bTXTXb. = –2XTY – 2XTXb = 0.
= –2XTY – 2XTXb = 0. . (2.4)
. (2.4) =
=  =
=  =
=  ,
, – оценённые по уравнению (2.2) значения зависимой переменной.
– оценённые по уравнению (2.2) значения зависимой переменной.


