Остановимся более подробно на свойствах полученных оценок. Относительно уравнения множественной регрессии можно высказать те же предположения 1 – 4, что и для простой регрессии (заменив независимую переменную векторов независимых переменных), в том числе и предположения, лежащие в основе теоремы Гаусса-Маркова.
Рассмотрим математическое ожидание полученных оценок.
M(b) = M( ) = M(
) = M( ) =
) = 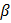 + M(
+ M(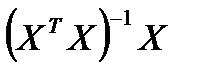 T
T 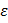 ) =
) =
= 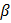 + (XTX)M(XT
+ (XTX)M(XT 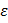 ) =
) = 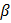 , т. к. M(XT
, т. к. M(XT 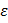 ) = XTM(
) = XTM(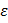 ) =0, если X и
) =0, если X и 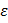 независимы.
независимы.
Здесь предполагается, что матрица Х детерминирована, а М(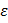 ) = 0. Таким образом, если регрессоры и остатки некоррелированны и математическое ожидание остатков равно нулю, то МНК-оценки являются несмещёнными. При доказательстве этого положения не использовались предположения 3 и 4 пункта 1.1, откуда следует, что МНК-оценки являются несмещённой до тех пор, пока регрессионные остатки имеют нулевое среднее и независимы от всех объясняющих переменных, даже если в них наблюдается гетероскедастичность и автокорреляция.
) = 0. Таким образом, если регрессоры и остатки некоррелированны и математическое ожидание остатков равно нулю, то МНК-оценки являются несмещёнными. При доказательстве этого положения не использовались предположения 3 и 4 пункта 1.1, откуда следует, что МНК-оценки являются несмещённой до тех пор, пока регрессионные остатки имеют нулевое среднее и независимы от всех объясняющих переменных, даже если в них наблюдается гетероскедастичность и автокорреляция.
Подсчитаем ковариационную матрицу полученных оценок. При этом будем иметь в виду, что ковариационная матрица остатков регрессии имеет вид  , т. к. регрессионные остатки взаимно независимы и гомоскедастичны (
, т. к. регрессионные остатки взаимно независимы и гомоскедастичны (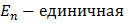 матрица размерности n
матрица размерности n 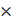 n):
n):
Cov(b) = М{(b- 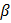 )(b-
)(b- 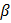 )T} = M{(XTX)-1XT
)T} = M{(XTX)-1XT  TX(XTX)-1} = (XTX)-1XT
TX(XTX)-1} = (XTX)-1XT  X(XTX)-1 =
X(XTX)-1 =  (XTX)-1, т. к. M(
(XTX)-1, т. к. M( T) =
T) =  .
.
Итак, Cov(b) =  (XTX)-1. На главной диагонали этой матрицы находятся дисперсии соответствующих оценок, т. е. D (
(XTX)-1. На главной диагонали этой матрицы находятся дисперсии соответствующих оценок, т. е. D (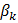 ) =
) =  .
.

 ) = M(
) = M( ) =
) = 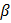 + M(
+ M(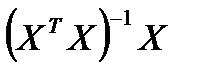 T
T 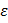 ) =
) = , т. к. регрессионные остатки взаимно независимы и гомоскедастичны (
, т. к. регрессионные остатки взаимно независимы и гомоскедастичны (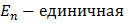 матрица размерности n
матрица размерности n 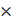 n):
n): TX(XTX)-1} = (XTX)-1XT
TX(XTX)-1} = (XTX)-1XT  X(XTX)-1 =
X(XTX)-1 =  (XTX)-1, т. к. M(
(XTX)-1, т. к. M(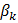 ) =
) =  .
.


