Мультиколлинеарность
Одним из условий классической регрессионной модели является предположение о линейной независимости объясняющих переменных, что означает независимость столбцов матрицы регрессоров X. Это обеспечивает неравенство нулю определителя матрицы ХТХ и существование обратной матрицы (XTX)-1, которая используется в МНК при вычислении оценок параметров уравнения регрессии ( На практике полная коллинеарность встречается редко, чаще приходится сталкиваться с ситуацией, когда анализируемые признаки тесно связаны друг с другом. Тогда говорят о наличии мультиколлинеарности. В этом случае МНК-оценка формально существует, но обладает «плохими» свойствами. Объясняется это тем, что определитель матрицы (XTX) в этом случае близок к нулю, а при вычислении обратной матрицы элементы союзной матрицы делятся на этот определитель, в результате чего все элементы обратной матрицы будут не оправдано большими. А они используются при вычислении стандартных ошибок оценок параметров уравнения регрессии. Как известно, Мультиколлинеарность может возникнуть в силу разных причин, например, при анализе временных рядов несколько независимых переменных могут иметь общий временной тренд или в качестве независимых переменных выступают лаговые значения одной и той же переменной и т. д. Нет однозначного метода решения проблемы мультиколлинеарности. Иногда достаточно удалить какую-либо переменную из уравнения, но при этом не всегда ясно, какая из них «лишняя». А если эта переменная значимо влияет на зависимую переменную, то это влияние перейдёт на остатки и они могут стать коррелированными, к тому же это может вызвать смещение оценок.
|

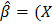 TX)-1XTY). При нарушении этого условия говорят, что имеет место совершенная мультиколлинеарность и тогда нельзя построить МНК-оценку параметров модели.
TX)-1XTY). При нарушении этого условия говорят, что имеет место совершенная мультиколлинеарность и тогда нельзя построить МНК-оценку параметров модели. =
=  , где
, где  – диагональные элементы матрицы
– диагональные элементы матрицы  TX)-1, а они большие по величине. В результате чего оценки рассчитываются с грубыми ошибками, что приводит к искажению смысла таких оценок (иногда даже по знаку). Кроме того, эти ошибки участвуют при вычислении t-статистик для проверки гипотез о равенстве нулю коэффициентов уравнения регрессии (
TX)-1, а они большие по величине. В результате чего оценки рассчитываются с грубыми ошибками, что приводит к искажению смысла таких оценок (иногда даже по знаку). Кроме того, эти ошибки участвуют при вычислении t-статистик для проверки гипотез о равенстве нулю коэффициентов уравнения регрессии ( ), поэтому часто приходится ошибочно не отклонять гипотезу о равенстве нулю коэффициентов регрессии.
), поэтому часто приходится ошибочно не отклонять гипотезу о равенстве нулю коэффициентов регрессии.


