Тестирование ошибки спецификации уравнения регрессии
Как уже отмечалось, среди предпосылок МНК присутствует предпосылка о нулевом математическом ожидании остатков регрессионной модели и, если при этом остатки и регрессоры независимы, оценки параметров уравнения регрессии будут несмещёнными. Тестирование предположения о том, что в рамках нормальной линейной модели M( При помощи этого критерия можно выявить: • наличие пропущенных переменных (т.е. невключение в правую часть уравнения некоторых существенных переменных); • неправильную функциональную форму представления переменных (например, использование логарифмов переменных вместо их уровней); • наличие корреляции между объясняющими переменными и остатками уравнения регрессии. Рассмотрим идею этого теста, реализованного в пакете EViews. В этом тесте сначала оценивается исходная модель и по ней находятся расчётные значения зависимой переменной Затем оценивается вспомогательная модель, в которую помимо исходных переменных включаются несколько слагаемых вида Например, исходная модель имеет вид В рамках этой модели проверяется гипотеза H0: Эту гипотезу можно тестировать с помощью обычного F-теста. Обычно этот тест применяется при небольших значениях r =1,2,3. Идея этого теста заключается в том, что добавлением нелинейных членов в уравнение регрессии не удаётся улучшить его качество.
2.2.6. Учёт некоторых нарушений стандартных предположений о модели
Рассмотрим кратко один из вариантов решения проблем, возникающих при наличии автокорреляции и гетероскедастичности в остатках регрессионных уравнений. Как уже отмечалось, в этих случаях МНК-оценки параметров уравнений регрессии будут состоятельными и несмещёнными, но несостоятельными и смещёнными могут оказаться ошибки этих оценок. В связи с этим одним из методов коррекции статистических выводов состоит в использовании обычных МНК-оценок, со скорректированными стандартными ошибками этих оценок, с учётом их автокорреляции и гетероскедастичности. Рассмотрим эти два случая по отдельности. Предположим, что после оценивания параметров модели каким-либо методом было выяснено, что имеет место гетероскедастичность остатков этой модели при отсутствии какой-либо автокорреляции. Поскольку сами оценки при этом будут несмещёнными, то для верных статистических выводов достаточно будет скорректировать стандартные ошибки этих оценок. Одним из вариантов получения скорректированных на гетероскедастичность стандартных ошибок Оценка Уайта строится на основе явного выражения для ковариационной матрицы вектора оценок коэффициентов линейной эконометрической модели, в которой ошибки хотя и имеют нулевые математические ожидания, но не являются одинаково распределёнными, т. е. с разными дисперсиями, но взаимно независимы. Тогда ковариационная матрица остатков примет вид Cov( Понятно, что это не единственный вариант корректировки последствий гетероскедастичности остатков уравнения регрессии. Иногда достаточно изменить вид зависимости или преобразовать переменные (например, перейти к логарифмам объясняемых переменных вместо их исходных значений). Пусть теперь имеем более сложный случай, когда остатки не только гетероскедастичны, но и автокоррелированы. Поскольку последствия автокорреляции в остатках аналогичны уже рассмотренным в случае их гетероскедастичности, можно воспользоваться аналогичной процедурой коррекции статистических выводов и при автокоррелированных остатках. Один из вариантов получения скорректированных на автокоррелированность и гетероскедастичность значений Следует отметить, что автокореляция в остатках может появиться и потому, что при выборе объясняющих переменных была пропущена значимая переменная, и её влияние на зависимую переменную будет отражаться на поведении остатков. Кроме того, автокорреляция в остатках может появиться и при не правильном выборе вида зависимости. Ясно, что в этих случаях простой коррекцией ошибок оценок не обойтись. Необходимо провести более тщательный анализ при определении спецификации уравнения регрессии. Подобные ошибки в спецификации уравнения регрессии вряд ли удастся нейтрализовать описанными методами.
Пример 2. Тестирование предпосылок МНК Проиллюстрируем вышеизложенные положения на условном примере, в котором описывается зависимость пятилетних процентных ставок (r60) от одномесячных (r1), квартальных (r3), полугодовых (r6) и годовых (r12) процентных ставок (данные взяты из М. Вербик, 2008). На рисунке 2.6 приведены графики этих переменных.
Рисунок 2.6 – Графики динамики анализируемых переменных
На рисунке 2.6 видим, что анализируемые переменные изменяются во времени почти параллельно, что может быть причиной их коллинеарности, в чём действительно убеждаемся, просмотрев матрицу парных коэффициентов корреляции (рисунок 2.7). Все коэффициенты корреляции между независимыми переменными оказались больше 0,9. В этом случае «доверять» коэффициентам уравнения не рекомендуется.
Рисунок 2.7. – Матрица парных коэффициентов корреляции
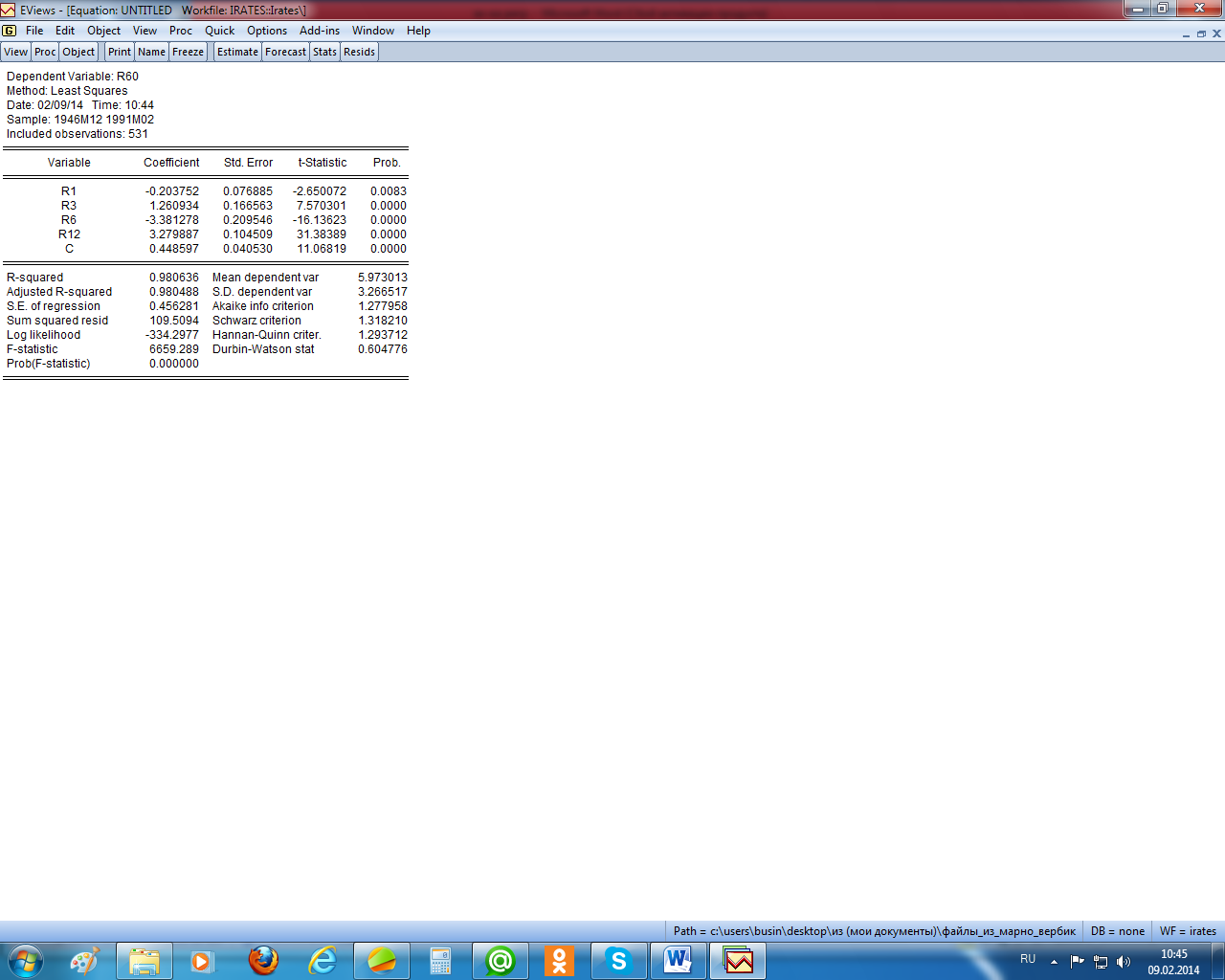
Рисунок 2.8 – «Полное» уравнение регрессии
Рисунок 2.9 – Уравнение регрессии с исключённой переменной
Как известно, мультиколлинеарность искажает смысл коэффициентов регрессии и делает их неустойчивыми. «Полное» уравнение регрессии не позволяет проследить последствия мультиколлинеарноси. Разве что малое значение статистики Дарбина – Уотсона указывает на наличие автокорреляции первого порядка (рисунок 2.8). Но относить этот факт на счёт мультиколлинеарности вряд ли корректно. Попробуем проверить устойчивость коэффициентов регрессии, удалив из регрессии одну из переменных. Пусть это будет r3 (рисунок 2.9). Как видим, действительно коэффициенты «сокращённого» уравнения существенно отличаются от коэффициентов исходного уравнения. Кроме того, что коэффициенты значимо отличаются от их исходных значений по величине, сменился даже знак коэффициента при переменной r1. При этом точность уравнения регрессии с исключённой переменной значимо не изменилась. Разве что уменьшилось значение статистики Дарбина – Уотсона, что означает, что имеет место существенная автокорреляция первого порядка.
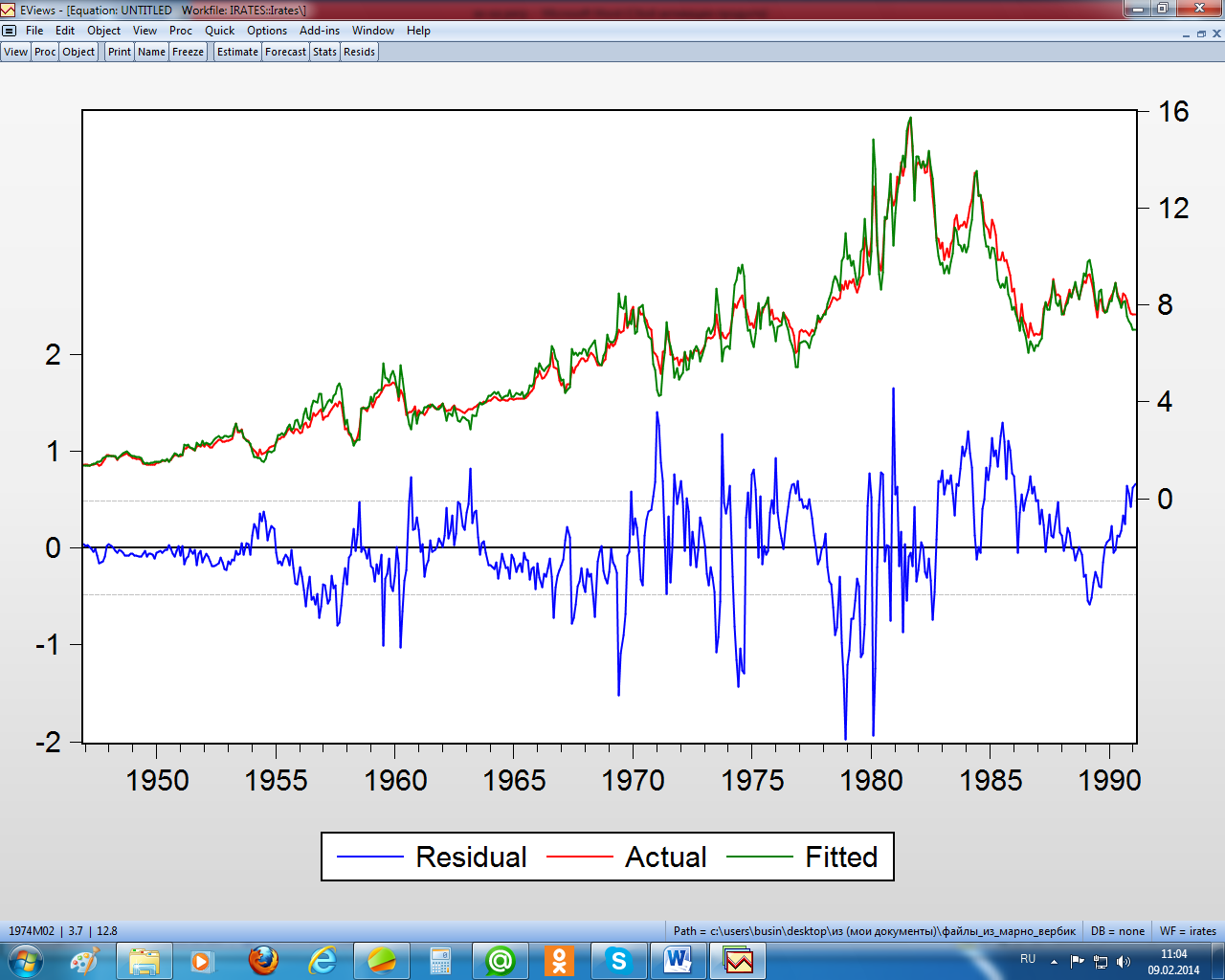
Рисунок 2.10 – Графики остатков, фактических и расчётных значений зависимой переменной
На рисунке 2.10 чётко просматривается наличие автокорреляции и гетероскедастичности остатков. Протестируем эти остатки по всем предпосылкам МНК.
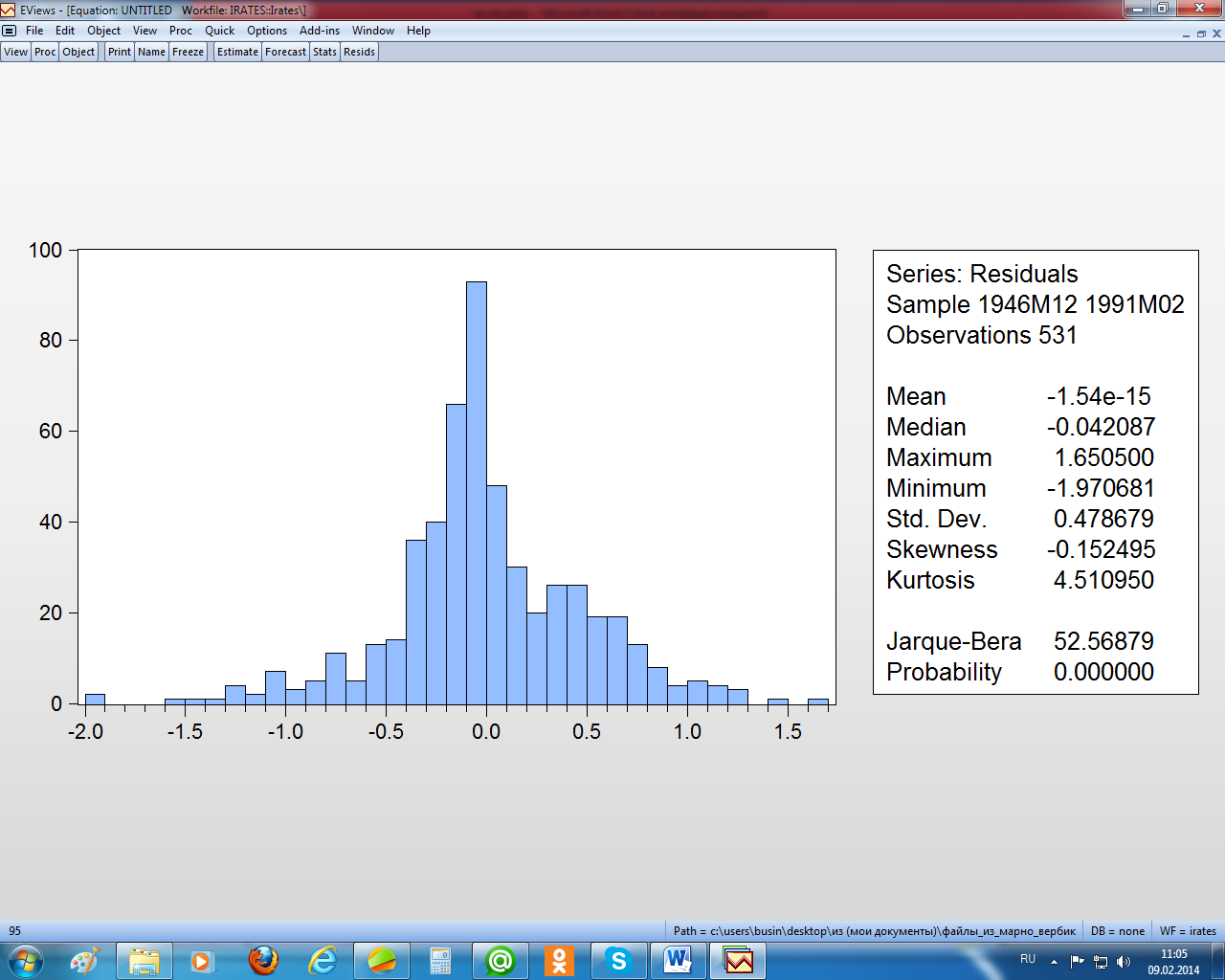
Рисунок 2.11 – Гистограмма остатков регрессии и тест Jarque – Bera
Сначала проверим их на нормальный закон распределения (рисунок 2.11). Тест Jarque – Bera показывает, что гипотезу о нормальном законе следует отклонить, т. к. расчётный уровень значимости (Probability) меньше 0,05. У этого распределения асимметрия отрицательна – более «тяжёлый» левый хвост распределения, а эксцесс значимо больше трёх – более островершинное распределение по сравнению с нормальным. Как уже отмечалось, значимое влияние на свойство оценок этот факт не оказывает.
Рисунок 2.12 – Тест Breusch – Godfrey на автокорреляцию остатков
Протестируем остатки на автокорреляцию на основе теста Breusch – Godfrey (рисунок 2.12). На второй строчке отчёта о тесте Obs*-squared – это nR2, расчётный уровень значимости для статистики теста – это Prob. Chi-Square (4). Для тестирования по этому тесту было выбрано 4 лаговых значения для остатков, т. е. тестировалась автокорреляция до 4–го порядка. Prob. Chi-Square(4) = 0,0, что меньше 0,05, значит гипотеза об отсутствии автокорреляции отклоняется. Просматривая уравнение теста, видим, что имеется автокорреляция первого и четвёртого порядков, т. к. коэффициенты при RESID(–1) и RESID(–4) значимо отличаются от нуля 0 (расчётный уровень значимости для них меньше 0,05). Автокорреляция первого порядка была видна и на основе статистики Дарбина – Уотсона, а здесь выяснилось, что ещё имеется автокорреляция более высокого порядка. Протестируем остатки на гетероскедастичность по тесту Уайта (Heteroskedasticity Test White – рисунок 2.13). В нашем случае nR2 = 96,46, расчётный уровень значимости меньше 0,05, следовательно, гипотезу о гомоскедастичности остатков отклоняем и по уравнению теста видим, что остатки зависят от произведений переменных r1, r12 и от r6, r12, а также от r122. Далее, протестируем уравнение регрессии на ошибку спецификации по Ramsey RESET-тесту (рисунок 2.14). Как видим, F-статистика теста равна 7,7 и расчётный уровень значимости (Probability) равен 0,0. Следовательно, гипотеза об отсутствии ошибки спецификации отклоняется. Из уравнения теста видно, что добавление двух нелинейных членов в уравнение регрессии несколько улучшило качество исходного уравнения (хоть и не значимо, но увеличились R2 и
Рисунок 2.13 – Тест White на гетероскедастичность остатков регрессии
Рисунок 2.14 – Ramsey RESET-тест
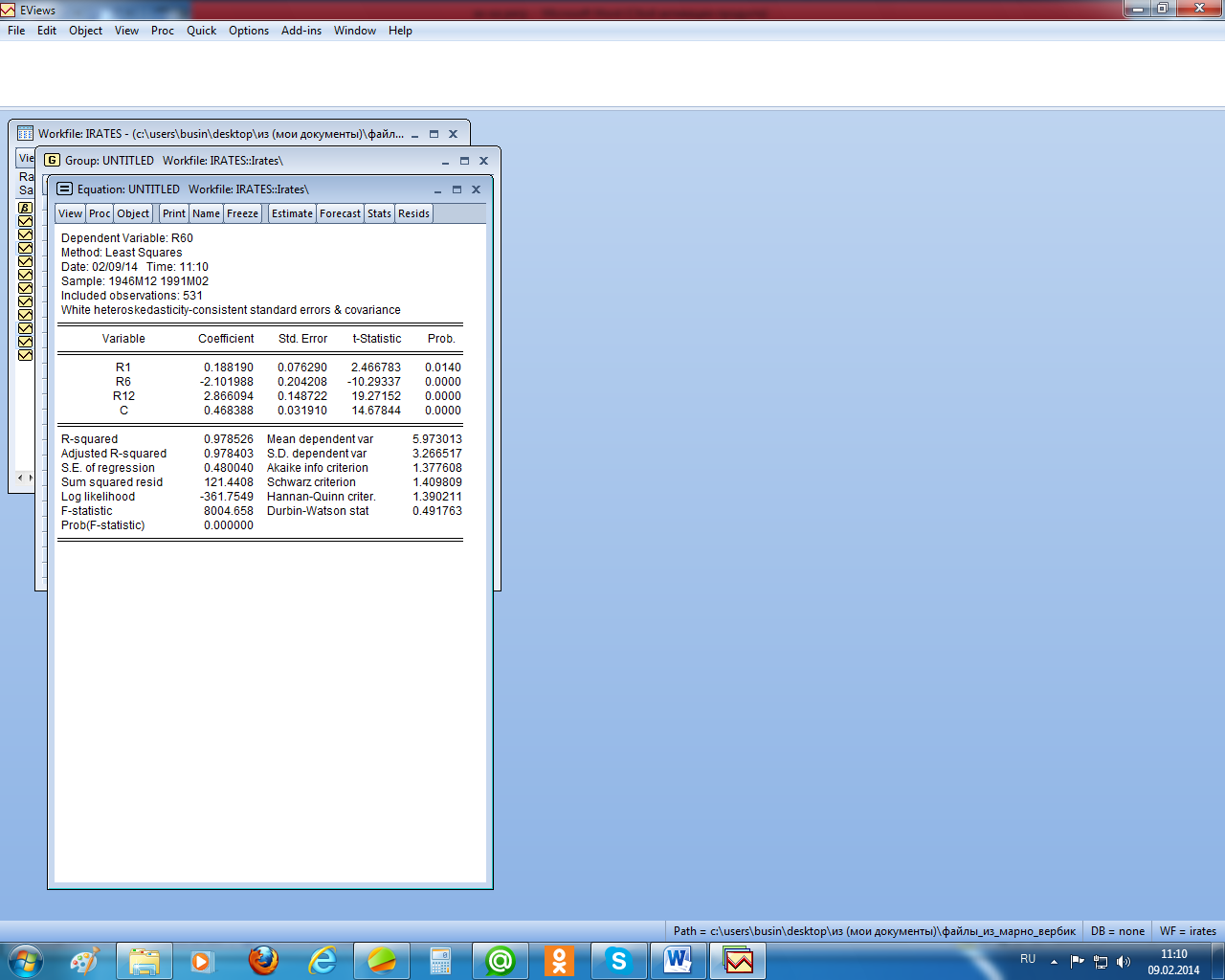
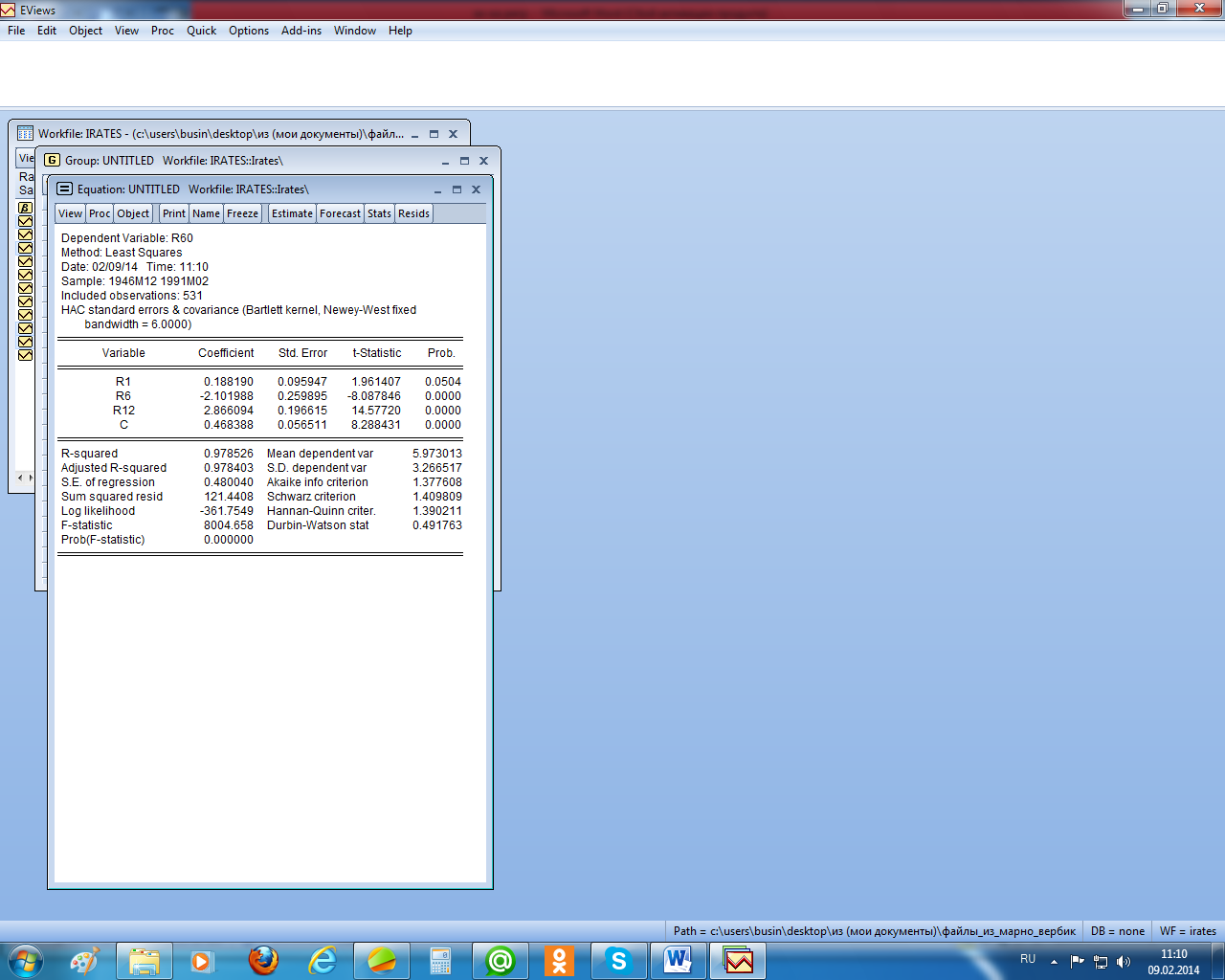
RESET-тест не указывает на конкретный тип ошибочной классификации. Это дело исследователя. В нашем случае высокий уровень автокоррелированности остатков может указывать на пропуск в уравнении регрессии значимой независимой переменной. Проиллюстрируем далее коррекцию стандартных ошибок МНК-оценок в случае их гетероскедастичности и автокоррелированности. Если оценки гетероскедастичны, но в них отсутствует какая-либо автокорреляция, то, как отмечалось, скорректировать их стандартные ошибки с учётом гетероскедастичности можно, используя стандартные ошибки в форме Уайта. Чтобы реализовать эту процедуру в EViews, надо в окне специализации уравнения регрессии выбрать заставку «Options» и там выбрать в позиции «Coefficient covariance matrix» нужный метод (рисунок 2.15). После выбора метода «White» получим (рисунок 2.16). Как видим на этом рисунке, стандартные ошибки были пересчитаны и стали больше по сравнению с аналогичными, вычисленными при использовании обычного МНК (рисунок 2.9). Значимость параметров при этом не изменилась. А теперь проведём корректировку отклонений с помощью метода Ньюи – Веста. Здесь кроме гетероскедастичности предполагается ещё и автокорреляция остатков (см. рисунок 2.17). Как видим, коррекция в этом случае оказалась более существенной, что привело даже к изменению значимости параметров – коэффициент при r1 оказался незначимым.
Рисунок 2.15 – Выбор процедур коррекции стандартных отклонений
Рисунок 2.16 – Стандартные ошибки в форме Уайта
Рисунок 2.17 – Стандартные ошибки в форме Ньюи – Веста 2.2.7. Обобщённый метод наименьших квадратов При рассмотрении классической регрессионной модели предполагалось, что случайные ошибки не коррелированы между собой и имеют постоянную дисперсию. Однако во многих ситуациях эти предположения не выполняются (не однородные объекты, зависимости во времени и т. п.). В этих случаях ковариационная матрица остатков не имеет вид В общем случае оценка параметров уравнения регрессии имеет вид Для применения ОМНК необходимо знать матрицу V, что на практике практически не реально (пришлось бы оценивать n(n – 1)/2 параметров при n наблюдениях). Если каким -либо образом (путём введения каких-либо условий на поведение остатков) удаётся оценить эту матрицу, то естественно использовать её в ОМНК для получения оценок вектора параметров модели. Такой подход составляет суть так называемого доступного ОМНК, одним из вариантов которого является взвешенный МНК. Взвешенный МНК представляет собой случай, когда ковариационная матрица V является диагональной (отсутствие какой-либо автокорреляции), а на главной диагонали находятся Здесь надо иметь в виду, что после оценки преобразованного уравнения, необходимо будет перейти в коэффициентам исходного уравнения. Например, если исходное уравнение имело вид y = a + b1x1 + b2x2 + e и выяснилось, что остатки пропорциональны x1, то преобразованное уравнение примет вид y/x1 =a(1/x1) + b1 + b2(x2/x1) + e/x1. В последнем уравнении свободный член уравнения (b1) и коэффициент при x1 (a) поменялись местами по отношению к исходному уравнению. После применения стандартного МНК к преобразованному уравнению необходимо будет вернуться к обозначениям исходного уравнения, а именно: считать а свободным членом исходного уравнения, а b1 – коэффициентом при x1.
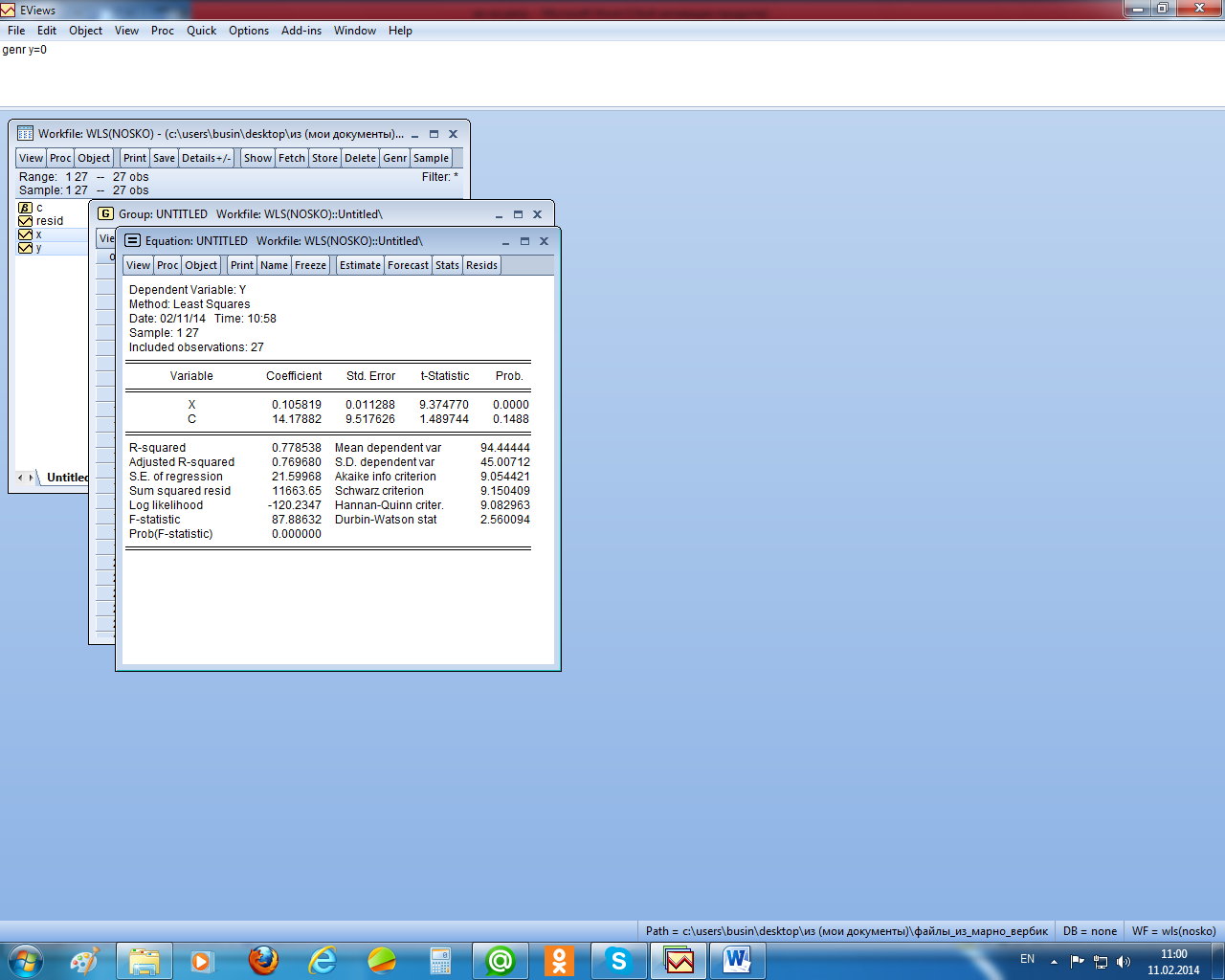
Пример 3. Взвешенный метод наименьших квадратов Проиллюстрируем идею взвешенного МНК на следующем примере (В. П. Носко, часть 1, 2011). Для исследования вопроса о зависимости количества руководящих работников от размера предприятия были собраны статистические данные по 27 предприятиям (х – численность персонала, у – количество руководителей). Уравнение регрессии приведено на рисунке 2.18.
Рисунок 2.18 – Отчёт об уравнении регрессии зависимости количества руководителей от численности персонала
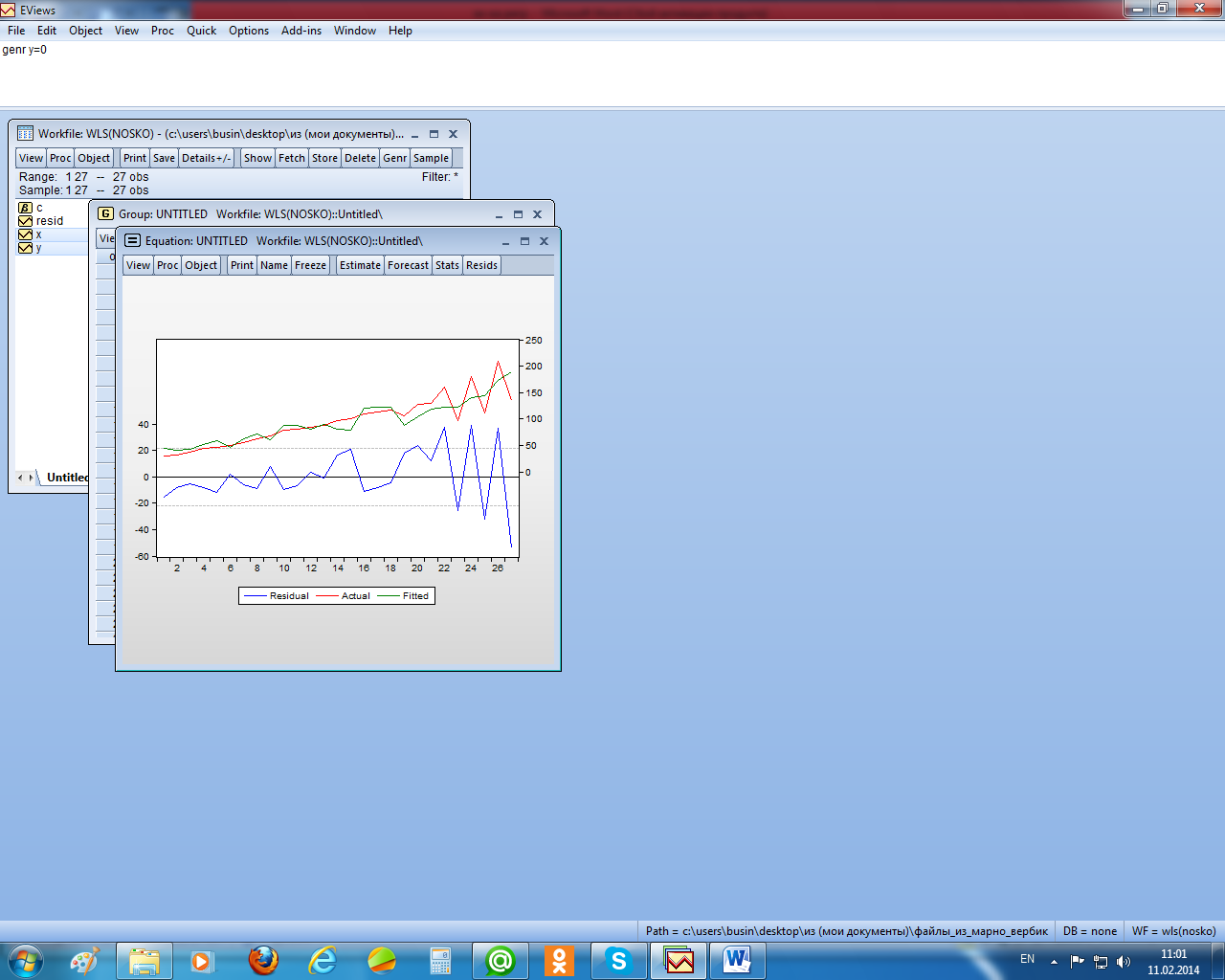
На рисунке 2.19 приведён график остатков для этого уравнения. Видно, что остатки гетероскедастичны. Причём остатки пропорциональны независимой переменной х. кроме того, тест Бройша – Годфри показал наличие в остатках автокорреляции второго порядка (рисунок 2.20).
Рисунок 2.19 – График остатков уравнения регрессии
Рисунок 2.20 – Тест Бройша – Годфри на автокорреляцию остатков
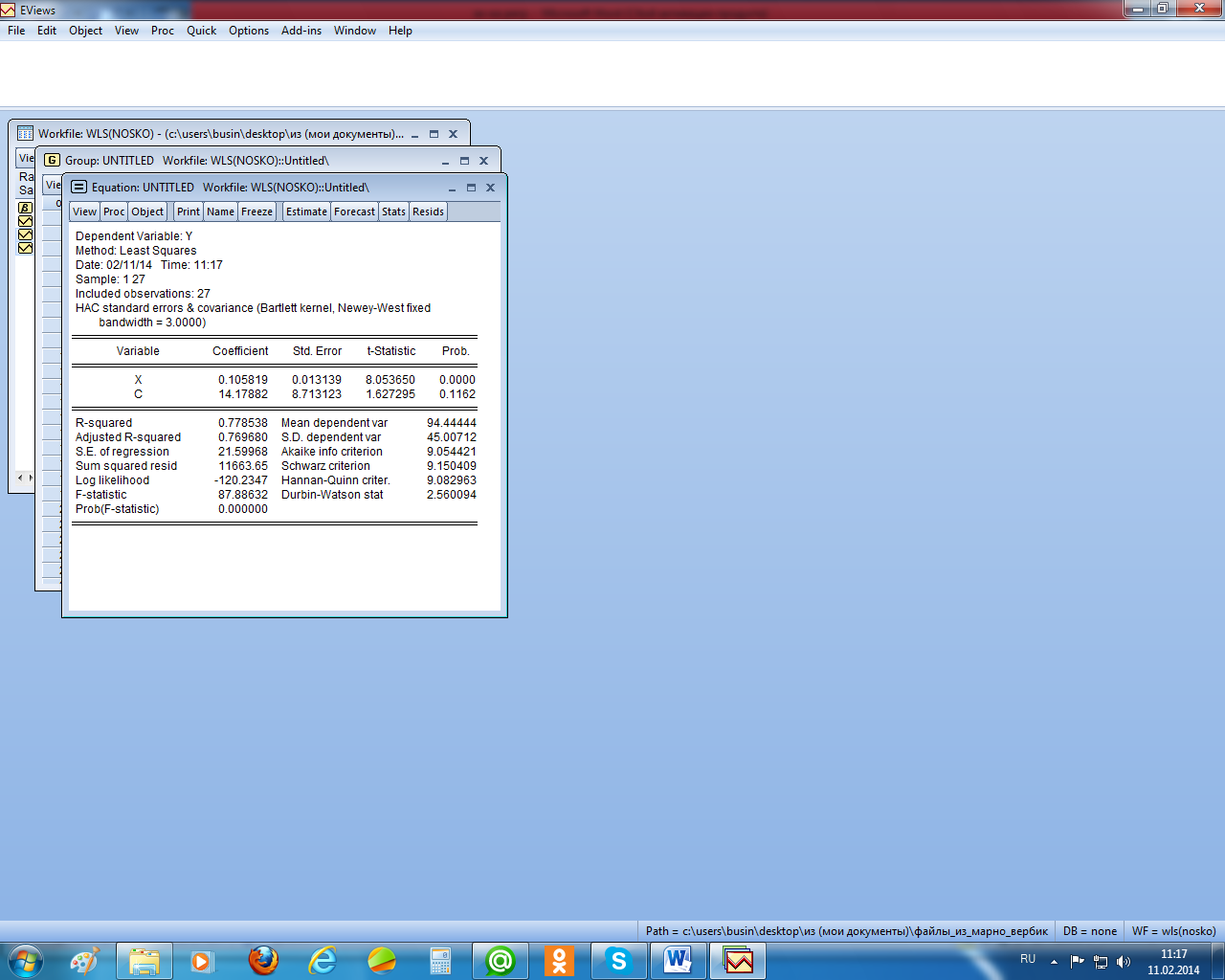
Поскольку остатки гетероскедастичны и автокоррелированы, проведём коррекцию их стандартных ошибок методом Ньюи – Веста (рисунок 2.21). Как видим, существенного изменения в оценках стандартных ошибках не произошло.
Рисунок 2.21 – Стандартные ошибки в форме Ньюи – Веста
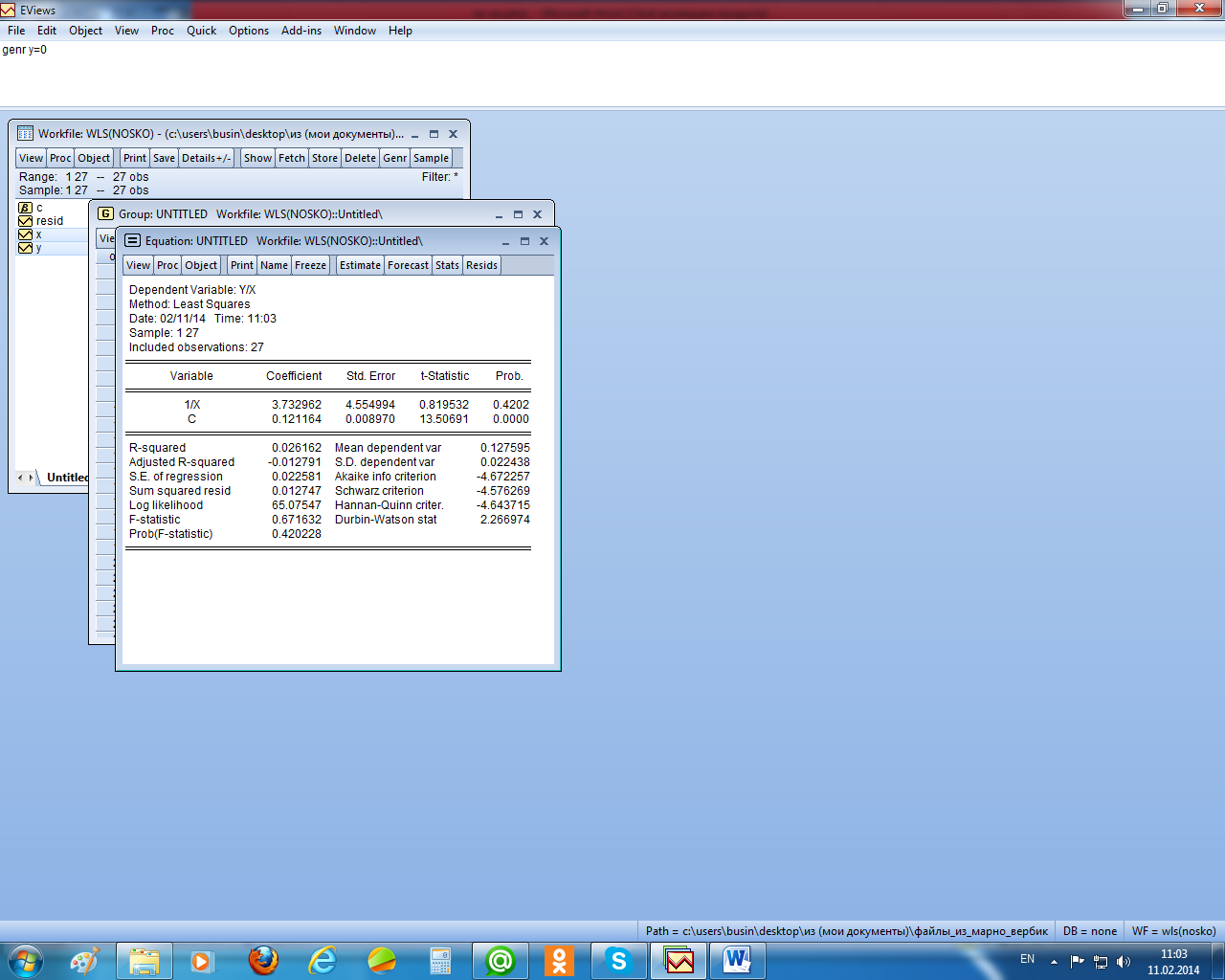
Для сравнения с проведённым исследованием применим взвешенный МНК, использовав в качестве весов 1/х, поскольку, как видно из рисунка 2.19, остатки пропорциональны независимой переменной. В результате получили следующее уравнение регрессии (рисунок 2.22).
Рисунок 2.22 – Взвешенный МНК
Как отмечалось, коэффициенты этого уравнения нужно интерпретировать в рамках исходного уравнения регрессии, т. е. константа – это коэффициент при х в исходном уравнении. Он незначимо отличается от коэффициента в исходной модели. Аналогично можно сказать и об оценке его стандартной ошибки. Различие же в свободных членах здесь не существенно, т. к. эти оценки незначимо отличаются от нуля (и там и там расчётный уровень значимости больше 0,05).
Рисунок 2.23 – График остатков преобразованного уравнения регрессии
А вот от гетероскедастичности в остатках этим методом (взвешенным МНК) удалось избавиться, их разброс вокруг нуля стал равномерным (рисунок 2.23).
|

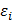 ) = 0, (i = 1,2,…, n) осуществляется на основе критерия Рэмси RESET (Ramsey̕ s Regression Equation Specification Error Test).
) = 0, (i = 1,2,…, n) осуществляется на основе критерия Рэмси RESET (Ramsey̕ s Regression Equation Specification Error Test).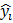 , (i=1,…,n).
, (i=1,…,n).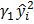 +
+ 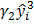 + …+
+ …+ 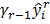 .
.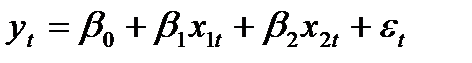 . Тогда вспомогательная модель будет вида
. Тогда вспомогательная модель будет вида 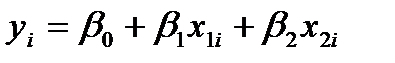 +
+ 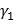 =…=
=…= 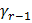 = 0.
= 0.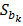 был предложен Уайтом и реализован в ряде пакетов анализа статистических данных, в том числе и в EViews. При этом удовлетворительные свойства скорректированной оценки Уайта (White estimator или White standard errors) гарантируются только при большом количестве наблюдений.
был предложен Уайтом и реализован в ряде пакетов анализа статистических данных, в том числе и в EViews. При этом удовлетворительные свойства скорректированной оценки Уайта (White estimator или White standard errors) гарантируются только при большом количестве наблюдений.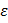 ) = diag(
) = diag( ), т. е. на главной диагонали проставлены дисперсии остатков (для каждого остатка своя дисперсия), а вне диагонали – нули (какая-либо автокорреляция отсутствует). Для оценки этих n дисперсий имеется всего n наблюдений. Тем не менее можно получить состоятельную оценку этой ковариационной матрицы, заменив неизвестные дисперсии ошибок, на квадраты остатков, полученных в результате оценки модели обычным МНК. Это приводит к оценке Уайта.
), т. е. на главной диагонали проставлены дисперсии остатков (для каждого остатка своя дисперсия), а вне диагонали – нули (какая-либо автокорреляция отсутствует). Для оценки этих n дисперсий имеется всего n наблюдений. Тем не менее можно получить состоятельную оценку этой ковариационной матрицы, заменив неизвестные дисперсии ошибок, на квадраты остатков, полученных в результате оценки модели обычным МНК. Это приводит к оценке Уайта.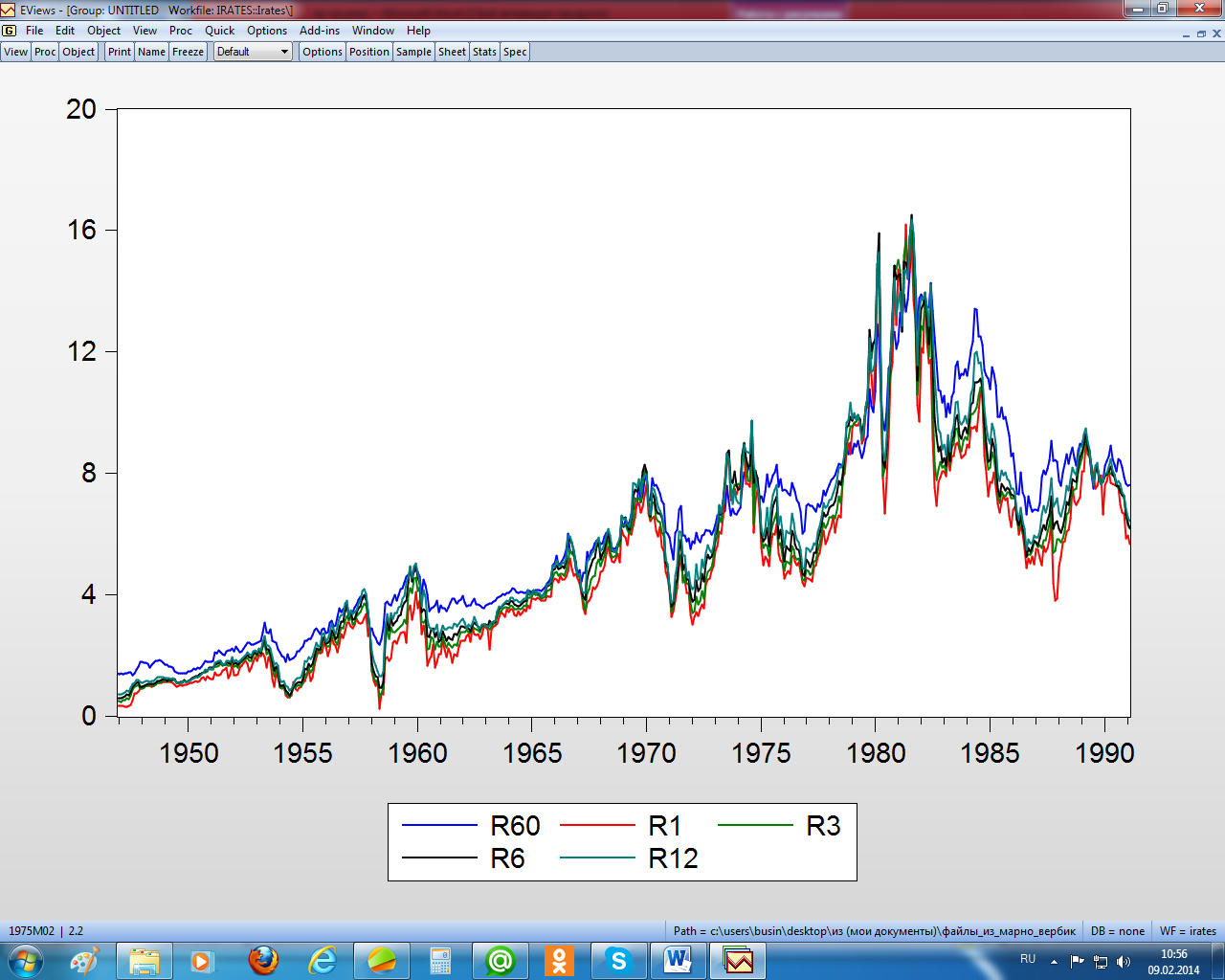



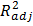 , уменьшился информационный критерий Шварца). Хотя автокорреляция в остатках усилилась (статистика Дарбина – Уотсона приблизилась к нулю).
, уменьшился информационный критерий Шварца). Хотя автокорреляция в остатках усилилась (статистика Дарбина – Уотсона приблизилась к нулю).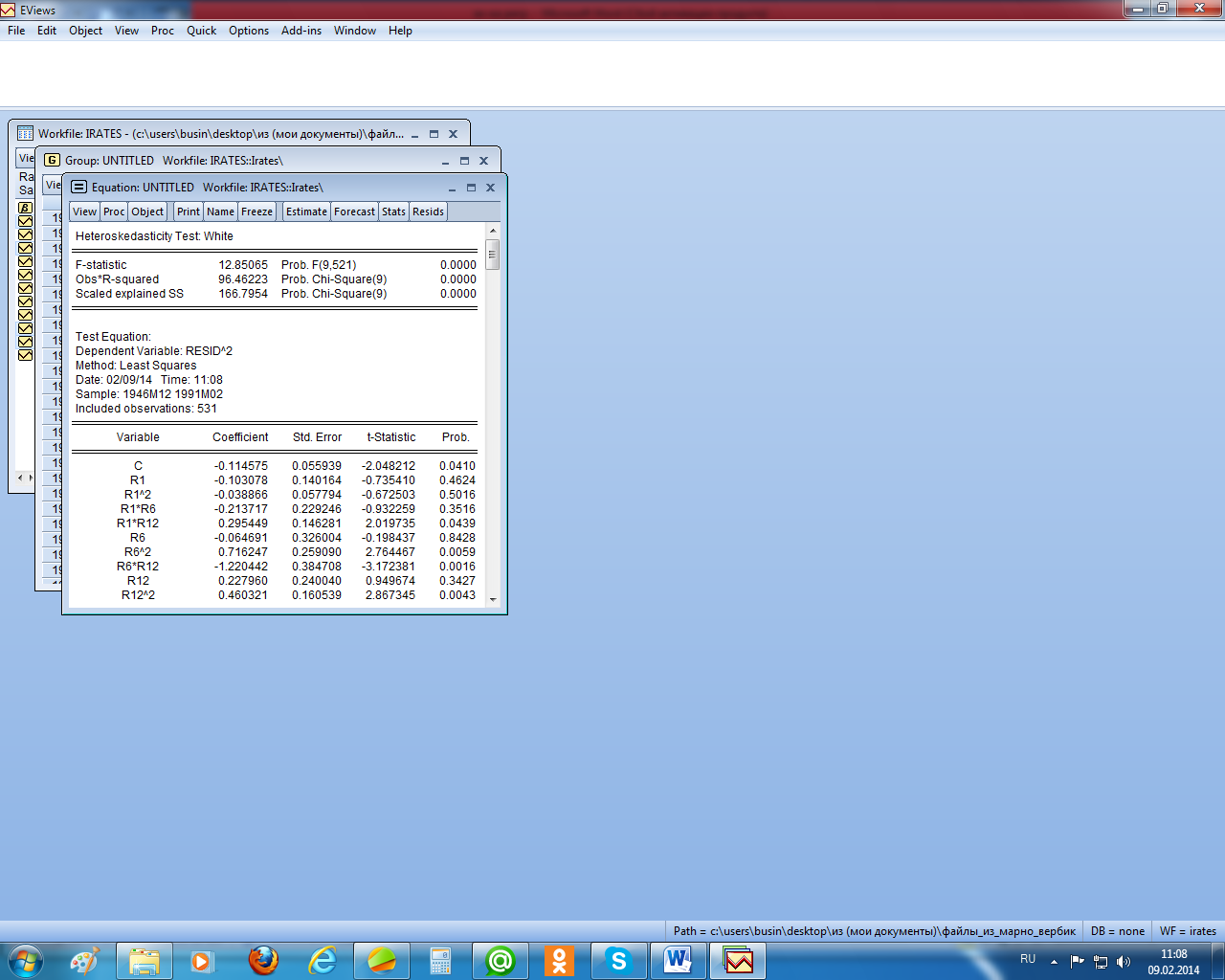


 , как это предполагалось раньше, а может быть произвольной симметричной положительно определённой матрицей V. С помощью линейного преобразования исходную систему можно свести к обычному регрессионному уравнению и построить для него МНК-оценку вектора коэффициентов. Эта оценка зависит от матрицы ковариаций остатков регрессии, а способ оценивания носит название обобщённого метода наименьших квадратов (ОМНК). Для ОМНК-оценки устанавливается аналог теоремы Гаусса –Маркова, а именно, доказывается, что в классе всех несмещённых линейных оценок она обладает наименьшей матрицей ковариаций (теорема Айткена).
, как это предполагалось раньше, а может быть произвольной симметричной положительно определённой матрицей V. С помощью линейного преобразования исходную систему можно свести к обычному регрессионному уравнению и построить для него МНК-оценку вектора коэффициентов. Эта оценка зависит от матрицы ковариаций остатков регрессии, а способ оценивания носит название обобщённого метода наименьших квадратов (ОМНК). Для ОМНК-оценки устанавливается аналог теоремы Гаусса –Маркова, а именно, доказывается, что в классе всех несмещённых линейных оценок она обладает наименьшей матрицей ковариаций (теорема Айткена).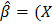 TV-1X)-1XTV-1Y, где V – ковариационная матрица остатков регрессионной модели. В классическом варианте, когда остатки гомоскедастичны и в них отсутствует какая-либо автокорреляция V =
TV-1X)-1XTV-1Y, где V – ковариационная матрица остатков регрессионной модели. В классическом варианте, когда остатки гомоскедастичны и в них отсутствует какая-либо автокорреляция V =  En, где En – единичная матрица размерности nхn, тогда
En, где En – единичная матрица размерности nхn, тогда 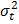 (наличие гетероскедастичности). В этом случае иногда возможно представление
(наличие гетероскедастичности). В этом случае иногда возможно представление 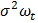 , где
, где  – некие веса. Особенно это удобно, если остатки уравнения регрессии пропорциональны значениям какой-либо переменной. Тогда в качестве весов можно взять значения этой переменной в выборке. Разделив все переменные анализируемого уравнения, можно применять обычный МНК к преобразованному уравнению. В случае удачного выбора весов можно успешно провести коррекцию на гетероскедастичность остатков уравнения регрессии.
– некие веса. Особенно это удобно, если остатки уравнения регрессии пропорциональны значениям какой-либо переменной. Тогда в качестве весов можно взять значения этой переменной в выборке. Разделив все переменные анализируемого уравнения, можно применять обычный МНК к преобразованному уравнению. В случае удачного выбора весов можно успешно провести коррекцию на гетероскедастичность остатков уравнения регрессии.