Фиктивные переменные в регрессионном анализе
Чтобы включить в регрессию в качестве независимых переменных качественные признаки, их надо оцифровать. Одним из методов их оцифровки является использование фиктивных переменных. Название не совсем удачное – никакие они не фиктивные, просто для этих целей более удобно использовать переменные, принимающие всего два значения – ноль или единица. Вот их и назвали фиктивными. Обычно качественная переменная может принимать несколько значений-уровней. Например, пол – мужской, женский; квалификация – высокая, средняя, низкая; сезонность – I, II, III и IV кварталы и т. д. Существует правило, согласно которому для оцифровки таких переменных нужно вводить количество фиктивных переменных, числом меньше на единицу, чем число уровней моделируемого показателя. Это необходимо для того, чтобы такие переменные не оказались бы линейно зависимыми. В наших примерах: пол – одна переменная, равная 1 для мужчин и 0 – для женщин. Квалификации имеет три уровня, значит, нужны две фиктивные переменные: например, z1 = 1 для высокого уровня, 0 – для других; z2 = 1 для среднего уровня, 0 – для других. Третью аналогичную переменную вводить нельзя, т. к. в этом случае они оказались бы линейно зависимыми (z1 + z2 + z3 = 1), определитель матрицы (XTX) обратился бы в нуль и найти обратную матрицу (XTX)-1 не удалось бы. Как известно, оценки параметров уравнения регрессии определяются из соотношения: Коэффициенты при фиктивных переменных показывают, насколько значение зависимой переменной отличается при анализируемом уровне по сравнению с отсутствующим уровнем. Например, если бы моделировался уровень зарплаты в зависимости от нескольких признаков и уровня квалификации, то коэффициент при z1 показал бы, насколько зарплата у специалистов с высоким уровнем квалификации отличается от зарплаты у специалиста с низким уровнем квалификации при прочих равных условиях, а коэффициент при z2 – аналогичный смысл для специалистов со средним уровнем квалификации. В случае с сезонностью пришлось бы вводить три фиктивных переменных (если рассматриваются квартальные данные) и коэффициенты при них показали бы, насколько величина зависимой переменной отличается для соответствующего квартала от уровня зависимой переменной для квартала, который не был введён при их оцифровке. Фиктивные переменные кроме того вводятся для моделирования структурных изменений в динамике изучаемых показателей при анализе временных рядов.
Пример 4. Стандартизированное уравнение регрессии и фиктивные переменные Рассмотрим пример использования стандартизированных коэффициентов и фиктивных переменных на примере анализа рынка двухкомнатных квартир на основе уравнения множественной регрессии при следующем наборе переменных: PRICE – цена; TOTSP – общая площадь; LIVSP – жилая площадь; KITSP – площадь кухни; DIST – расстояние до центра города; WALK – равна 1, если до станции метро можно дойти пешком и равна 0, если надо воспользоваться общественным транспортом; BRICK – равна 1, если дом кирпичный и равна 0, если панельный; FLOOR – равна 1, если квартира не на первом и не на последнем этаже и равна 0 в противном случае; TEL – равна 1, если в квартире есть телефон и равна 1, если нет; BAL – равна 1, если есть балкон и равна 0, если балкона нет. Расчёты проведены с помощью ППП STATISTICA (рисунок 2.23). Наличие b-коэффициентов позволяет упорядочить переменные по степени их влияния на зависимую переменную. Проведем краткий анализ результатов расчётов. На основе статистики Фишера делаем вывод о значимости уравнения регрессии (р-level < 0,05). Обработана информация о 6 286 квартирах (n–m–1 = 6 276, а m = 9). Все коэффициенты уравнения регрессии (кроме при переменной BAL) значимы (р-величины для них < 0,05), а наличие или отсутствие балкона в этом случае существенно не сказывается на цене квартиры.
Рисунок 2.24 – Отчёт о рынке квартир на основе ППП STATISTICA
Коэффициент множественной детерминации равен 52%, следовательно, включённые в регрессию переменные обусловливают изменение цены на 52 %, а остальные 48 % изменения цены квартиры зависят от неучтённых факторов. В том числе и от случайных колебаний цены. Каждый из коэффициентов при переменной показывает, насколько изменится цена квартиры (при прочих равных условиях), если данная переменная изменится на единицу. Так, например, при изменении общей площади на 1 кв. м цена квартиры в среднем изменится на 0,791 у.е., а при удалении квартиры от центра города на 1 км цена квартиры в среднем уменьшится на 0,596 у.е. и т. д. Фиктивные переменные (последние 5) показывают, на сколько в среднем изменится цена квартиры, если перейти с одного уровня этой переменной на другой. Так, например, если дом кирпичный, то квартира в нем в среднем на 3,104 у. е. дороже, чем такая же в панельном доме, а наличие телефона в квартире поднимает ее цену в среднем на 1,493 у. е. и т. п. На основе b-коэффициентов можно сделать следующие выводы. Наибольшим b-коэффициентом, равным 0,514 является коэффициент при переменной «общая площадь», следовательно в первую очередь цена квартиры формируется под влиянием её общей площади. Следующий фактор по степени влияния на изменение цены квартиры является расстояние до центра города, затем материал, из которого построен дом, затем площадь кухни и т. д.
|

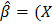 TX)-1XTY).
TX)-1XTY).



