Системы одновременных уравнений
Многие экономические взаимосвязи допускают моделирование одним уравнением. В этом случае предполагается, что между независимыми переменными хi и зависимой переменной у существует только прямая связь: хi Применение отдельных уравнений регрессии в большинстве случаев предполагает, что независимые переменные можно изменять независимо друг от друга. Однако на практике изменение одной переменной не может происходить при неизменности других. Поэтому отдельно взятое уравнение не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Поэтому при исследовании социально-экономических явлений важное место занимает проблема описания связей между переменными не одним, а несколькими уравнениями. Отсюда возникла необходимость в использовании систем эконометрических уравнений. Рассмотрим кратко проблемы, возникающие при анализе систем эконометрических уравнений на примере кейнсианской модели формирования доходов. Данная модель строится в предположении, что рассматривается закрытая экономика без государственных расходов: функция потребления тождество где
Коэффициент Особенность этой системы уравнений заключается в том, что в первом уравнении совокупный доход не является независимой переменной, а определяется вторым уравнением, которое является в этой модели определяющим уравнением для закрытой экономики и указывает, что совокупное потребление и совокупные инвестиции в сумме должны равняться совокупному доходу. В дальнейшем переменные, определяемые вне модели, будем называть экзогенными, а те из них, которые определяются на основе модели, – эндогенными. Таким образом, Будем предполагать, что остатки Тот факт, что
|

 у. Отсюда и терминология – зависимая и независимые переменные: у зависит от значений хi, а хi не зависят от значений у.
у. Отсюда и терминология – зависимая и независимые переменные: у зависит от значений хi, а хi не зависят от значений у. =
= 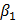 +
+  +
+ 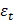 ;
; =
=  ,
,

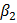 интерпретируется как предельная склонность к потреблению (0
интерпретируется как предельная склонность к потреблению (0  и показывает, насколько больше люди будут потреблять, если их доход увеличится на единицу.
и показывает, насколько больше люди будут потреблять, если их доход увеличится на единицу. эндогенные переменные (определяются в модели совместно), а инвестиции
эндогенные переменные (определяются в модели совместно), а инвестиции  , а
, а 


