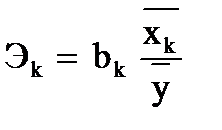Стандартизованное уравнение множественной регрессии
Коэффициенты уравнения регрессии, как и всякие абсолютные показатели, не могут быть использованы в сравнительном анализе, если единицы измерения соответствующих переменных различны. Например, если y – расходы семьи на питание, х1 – размер семьи, а х2 – общий доход семьи, и мы определяем зависимость типа Сопоставимость коэффициентов уравнения регрессии достигается при рассмотрении стандартизованного уравнения регрессии: y0 = b1x10 + b2x20 + … + bmxm0 + е, где y0 и x0k – стандартизованные значения переменных y и xk:
Sy и S bk (k=
b-коэффициенты уравнения регрессии в стандартизованном масштабе создают реальное представление о воздействии независимых переменных на моделируемый показатель. Если величина b-коэффициента для какой-либо переменной превышает значение соответствующего b-коэффициента для другой переменной, то влияние первой переменной на изменение результативного показателя следует признать более существенным. Следует иметь в виду, что стандартизированное уравнение регрессии в силу центрирования переменных не имеет свободного члена по построению. Для простой регрессии b-коэффициент совпадает с коэффициентом парной корреляции, что позволяет придать коэффициенту парной корреляции смысловое значение. При анализе воздействия показателей, включённых в уравнение регрессии, на моделируемый признак, наравне с b-коэффициентами используются также коэффициенты эластичности. Например, показатель средней эластичности рассчитывается по формуле
и показывает, на сколько процентов в среднем изменится зависимая переменная, если среднее значение соответствующей независимой переменной изменится на один процент (при прочих равных условиях).
|

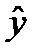 = a + b1 x1 + b2 x2 и b2 > b1, то это не значит, что x2 сильнее влияет на y, чем х1, т. к. b2 – это изменение расходов семьи при изменении доходов на 1 руб., а b1 – изменение расходов при изменении размера семьи на 1 человека.
= a + b1 x1 + b2 x2 и b2 > b1, то это не значит, что x2 сильнее влияет на y, чем х1, т. к. b2 – это изменение расходов семьи при изменении доходов на 1 руб., а b1 – изменение расходов при изменении размера семьи на 1 человека.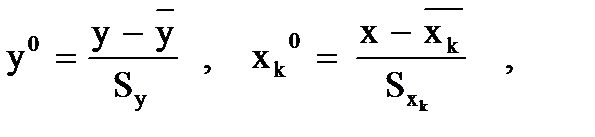
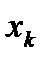 – стандартные отклонения переменных y и xk,
– стандартные отклонения переменных y и xk,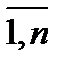 ) – b-коэффициенты уравнения регрессии (но не параметры уравнения регрессии, в отличие от приведенных ранее обозначений). b-коэффициенты показывают, на какую часть своего стандартного отклонения (Sy) изменится зависимая переменная y, если независимая переменная xk изменится на величину своего стандартного отклонения (S
) – b-коэффициенты уравнения регрессии (но не параметры уравнения регрессии, в отличие от приведенных ранее обозначений). b-коэффициенты показывают, на какую часть своего стандартного отклонения (Sy) изменится зависимая переменная y, если независимая переменная xk изменится на величину своего стандартного отклонения (S  ). Оценки параметров уравнения регрессии в абсолютных показателях (bk) и β-коэффициенты связаны соотношением:
). Оценки параметров уравнения регрессии в абсолютных показателях (bk) и β-коэффициенты связаны соотношением: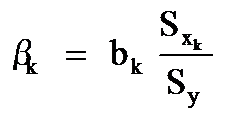 .
.