Пошаговый регрессионный анализ
Отбор переменных в уравнение множественной регрессии может осуществляться в несколько этапов. На первом этапе подобный отбор осуществляется исходя из качественного анализа изучаемого социально-экономического явления, без каких бы то ни было ограничений на переменные. На втором этапе на основе, например, анализа матрицы парных коэффициентов корреляции можно отсеять незначимые факторные переменные, если это не входит в противоречие с логикой изучаемого явления. И только на третьем этапе провести строгий отбор с использованием метода пошагового выбора переменных. При использовании этого метода отбор переменных происходит исходя только из формальных статистических критериев. Это основной недостаток метода. Подобные процедуры включены во многие статистические пакеты прикладных программ и предусматривают три варианта их реализации. Процедура “вперёд” (Forward) начинает «работать» с пустой моделью и последовательно включает в модель только значимые переменные. При этом на каждом шаге значимость каждой переменной определяется заново. Осуществляется это в разных программах по-разному, например, в Statgraphics на основе коэффициентов частной корреляции и рассчитанных для них статистик Фишера, а в EViews – либо на основе t-статистик, либо на основе p-value. Процедура включения переменных в модель заканчивается, если на очередном шаге наибольшее значение критерия Фишера или t-статистики (p-value) будет меньше граничного. Граничное значение либо устанавливается исследователем, либо определяется по умолчанию. Если в результате реализации этого метода переменная на каком-либо шаге была включена в уравнение, то она там остаётся до конечного шага алгоритма, даже если она потом окажется незначимой, поэтому в этом варианте процедуры пошаговой регрессии есть риск включить в регрессию незначимую переменную. Процедура ”назад” (Backward) начинает «работать» с полной моделью и последовательно исключает из неё незначимые переменные. Значимость оставшихся переменных здесь пересчитывается также на каждом шаге. В этом случае на каждом шаге из уравнения регрессии будут исключаться только незначимые независимые переменные. Если в этой процедуре переменная на каком-либо шаге была исключена из уравнения, но потом на каком-то шаге она стала значимой, то она не будет включена в уравнения до конца работы алгоритма, поскольку в дальнейшем анализе она не участвует, поэтому здесь есть риск исключить из регрессии значимую переменную. Пошаговая процедура (Stepwise) включения-исключения переменных состоит в сочетании двух уже рассмотренных методов. Здесь после очередного включения-исключения переменной происходит перерасчёт значимости и включённых и исключённых переменных и, если какая-либо ранее включённая (исключённая) переменная оказывается незначимой (значимой), то она исключается из уравнения или включается в него. В большинстве случаев эти три метода дают одинаковый конечный результат. Применение метода пошагового выбора переменных позволяет упростить уравнение регрессии без значимого ухудшения его точности. К тому же подобные процедуры исключают возможность включения в регрессию коллинеарных факторных переменных.
Пример 6. Пошаговый регрессионный анализ Рассмотрим пример анализа объёма реализации продукции фирмой (у) в зависимости от расходов на рекламу (х1), цены продукции (х2) в фирме и у конкурента (х3), а также от индекса потребительских расходов (х4) за 4 года поквартально. Расчёты будем вести в EViews, Оценённое уравнение регрессии с использованием обычного МНК представлено на рисунке 2.31.
Рисунок 2.33 – Отчёт об использовании обычного МНК
Как видим из отчёта (рисунок 2.31), две переменные в уравнении регрессии незначимы, т. е. объём реализации значимо не зависит от цены продукции на фирме и у конкурента. Проведём пошаговый регрессионный анализ, используя процедуру «назад», которая последовательно будет исключать из регрессии незначимые переменные. С этой целью в окне спецификации уравнения в позиции «Method» выберем процедуру «STEPLS – Stepwise Least Squares» (пошаговый МНК) (рисунок 2.34). В первом окне устанавливаем имя зависимой переменной и константу, а во втором – список независимых переменных. После этого в заставке «Options» (рисунок 2.35) выбираем метод реализации пошагового МНК «Backwards
Рисунок 2.34 – Выбор процедуры пошагового МНК
Рисунок 2.35 – Выбор метода пошагового МНК и критерия остановки
Реализация выбранного метода показана на рисунке 2.36. Как видим, в уравнении регрессии осталось две переменные (х4 и х1) и обе они значимые. И хотя R-squared несколько уменьшился, по информационным критериям полученное уравнение предпочтительнее исходного (значения этих критериев уменьшилось). В нижней части отчёта указана последовательность исключения переменных из уравнения, а в примечании указано, что расчётный уровень значимости (p-value) и последующий тесты для выводимых переменных не отражены в процедуре пошагового выбора.
Рисунок 2.36 – Отчёт о пошаговом МНК
|


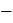 назад» и критерий остановки работы метода по p-value = 0.05. Другие установки этого диалогового окна здесь не обсуждаются.
назад» и критерий остановки работы метода по p-value = 0.05. Другие установки этого диалогового окна здесь не обсуждаются.