Тестирование остатков на нормальный закон распределения
Тестов на нормальный закон распределения разработано достаточно много. У каждого из них есть свои преимущества и недостатки. Остановимся здесь на одном из них, реализованном в эконометрическом пакете EViews. Этот тест носит название своих авторов (Jarque – Bera test). Статистика Jarque – Bera (JB) (Харке – Бера) предназначена для проверки нулевой гипотезы о нормальном законе распределения для значений рассматриваемой переменной. Статистика (JB) в EViews рассчитывается из соотношения JB = (n – k) где S – асимметрия; К – эксцесс; n – объём выборки; k – число оцениваемых параметров в регрессии. Известно, что для нормального закона распределения S = 0, К = 3, тогда и JB = 0. JB-статистика в предположении верности нулевой гипотезы имеет хи-квадрат распределение с двумя степенями свободы ( Отметим ещё раз, что критерии Дарбина – Уотсона и Голдфелда – Квандта являются точными (неасимптотическими) в том смысле, что они непосредственно учитывают количество наблюдений в выборке. В противоположность этому критерии Харке – Бера, Бройша – Годфри и Уайта являются асимптотическими и хорошо приближаются распределением хи-квадрат только при большом объёме наблюдений. Поэтому вполне полагаться на результаты применения последних можно только при больших объёмах выборки..
|


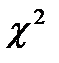 (2)). И если расчётное значение статистики JB окажется больше критического значения статистики хи–квадрат при фиксированном уровне значимости
(2)). И если расчётное значение статистики JB окажется больше критического значения статистики хи–квадрат при фиксированном уровне значимости  , то гипотеза о нормальном законе распределения отклоняется (при этом Probability для JB будет меньше
, то гипотеза о нормальном законе распределения отклоняется (при этом Probability для JB будет меньше 


