Анализ остатков уравнения множественной регрессии на автокорреляцию
Как уже отмечалось, одной из предпосылок МНК является независимость отклонений e = y – 1) в регрессионную модель не введен значимый факторный признак и его изменение приводит к значимому изменению последовательных остаточных величин; 2) в регрессионную модель не включено несколько незначимых факторов, но их изменения совпадают по направлению и фазе, и их суммарное воздействие приводит к значимому изменению последовательных остатков: 3) неверно выбран вид зависимости между анализируемыми переменными; 4) автокорреляция остатков может возникнуть не в результате ошибок, допущенных при построении регрессионной модели, а вследствие особенностей внутренней структуры случайных компонент (например, при описании регрессией динамических рядов). Анализ остатков на автокорреляцию, как и в случае парной регрессии, можно проводить на основе критерия Дарбина – Уотсона (Durbin – Watson test). Табличные значения этого критерия определяются при известных n (объём выборки), m (число независимых переменных) и α (принятый уровень значимости). Дальнейшие исследования – по аналогии с простой регрессией. Если с помощью этого критерия обнаружена существенная автокорреляция остатков, то необходимо признать наличие проблемы в определении спецификации уравнения и либо пересмотреть набор включаемых в уравнение регрессий переменных, либо форму регрессионной зависимости. В б о льшей степени такой анализ актуален при рассмотрении регрессии на временные ряды. Как уже отмечалось, статистика Дарбина – Уотсона обладает рядом недостатков и в некоторых случаях её использование проблематично: тестируется только автокорреляция первого порядка, нельзя использовать, если среди регрессоров есть лаговые значения зависимой переменной, необходимо присутствие в регрессии константы и т. д. Поэтому разработаны альтернативные тесты для проверки автокорреляции в остаточных членах уравнения регрессии, лишённые таких недостатков. Рассмотрим один из них реализованный в пакете EViews. Этот тест носит имя своих авторов – тест Бройша – Годфри (Breusch – Godfrey test). Идея этого теста в следующем. Сначала обычным МНК оценивается исходное уравнение регрессии. Затем составляется вспомогательное уравнение регрессии, в котором зависимой переменной являются остатки исходного уравнения, а независимыми – константа, исходные независимые переменные и лаговые значения остатков исходного уравнения. Число лаговых значений остатков во вспомогательном уравнении определяется эмпирически. Затем оценивается вспомогательное уравнение и рассчитывается статистика Опишем этот тест на примере уравнения регрессии с двумя переменными. Пусть рассматривается следующее исходное уравнение:
Чтобы протестировать остаточные члены этого уравнения на автокорреляцию (на серийную корреляцию) по тесту Бройша – Годфри, оценим исходное уравнение стандартным МНК и составим вспомогательное уравнение
Этим тестом проверяется нулевая гипотеза Отметим ещё раз, что тестирование остатков регрессии на автокорреляцию в основном рекомендуется, если анализируются временные ряды. При анализе пространственной информации изучаются в основном случайные выборки, и понятие порядка автокорреляции теряет смысл.
|

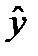 друг от друга. Если это условие нарушено, то говорят об автокорреляции остатков. Причин возникновения автокорреляции в остатках для уравнения множественной регрессии несколько. Выделим среди них следующие:
друг от друга. Если это условие нарушено, то говорят об автокорреляции остатков. Причин возникновения автокорреляции в остатках для уравнения множественной регрессии несколько. Выделим среди них следующие: , где n – объём выборки, а
, где n – объём выборки, а  – коэффициент множественной детерминации вспомогательного уравнения. Доказано, что если автокорреляция в остатках исходного уравнения отсутствует, то статистика
– коэффициент множественной детерминации вспомогательного уравнения. Доказано, что если автокорреляция в остатках исходного уравнения отсутствует, то статистика  (хи-квадрат распределению с p степенями свободы), где p – максимальное число лаговых значений остатков во вспомогательном уравнении. Если окажется, что
(хи-квадрат распределению с p степенями свободы), где p – максимальное число лаговых значений остатков во вспомогательном уравнении. Если окажется, что  , то гипотеза об отсутствии автокорреляции в остатках отклоняется.
, то гипотеза об отсутствии автокорреляции в остатках отклоняется.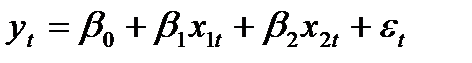 .
. .
.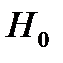 :
:  , против альтернативной гипотезы
, против альтернативной гипотезы  : не все
: не все 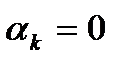 . После оценки вспомогательной регрессии проверяется неравенство
. После оценки вспомогательной регрессии проверяется неравенство 


