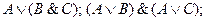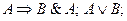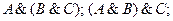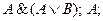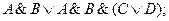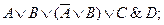Знание правил замены операций импликации и эквивалентности помогает правильно построить отрицание импликации.

Рассмотрим пример. Пусть дано высказывание: Е = Неверно, что если я выиграю конкурс, то получу приз. Пусть А = Я выиграю конкурс, В = Я получу приз. Тогда , т.е. Е = Я выиграю конкурс, но приз не получу.

УПРОЩЕНИЕ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ

Упрощение сложных высказываний – это замена их на равносильные на основе законов алгебры высказываний с целью получения высказываний более простой формы.

При упрощении сложных высказываний рекомендуется использовать следующие основные приемы замены отдельной переменной или константы формулой:

	по свойствам констант
	по закону исключенного третьего
	по закону непротиворечия
	по закону идемпотентности
	по закону двойного отрицания

Пример 3.

Требуется упростить: .

По закону дистрибутивности вынесем А за скобки: .

 

Пример 4.

Требуется упростить: .

В данном случае воспользуемся законом двойного отрицания.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Перечислите существенные признаки, составляющие содержание понятий:

а) квинтэссенция;

б) добродетель;

в) истина;

г) ложь.

Подсказка: посмотрите толковые словари.

1. Определите объемы понятий:

а) столица Украины;

б) столица;

в) город;

г) знаменитый полководец;

д) бесконечность;

е) Змей Горыныч.

3. Оцените правильность следующего рассуждения: Сидящий встал; кто встал, тот стоит; значит, сидящий стоит.

4. Отличаются ли содержания понятий «истина» и «логическая правильность»?

5. В чем заключается основной принцип формальной логики? Поясните на конкретном примере.

6. Выведите, если это возможно, заключение из каждой пары посылок:

а) Тем, кто лыс, расческа не нужна.

Ни одна ящерица не имеет волос.

б) Ни один добрый поступок не является незаконным.

Все, что законно можно делать без страха.

в) Некоторые уроки трудны.

Все, что трудно, требует внимания.

7. Определите, какие из ниже приведенных фраз являются высказываниями с точки зрения алгебры логики. Определите значение высказывания (истина или ложь):

а) Число 8456 является совершенным.

б) Без труда не выловишь и рыбку из пруда.

в) Как хорошо быть генералом!

г) Революция может быть мирной и немирной.

д) Зрение бывает нормальное, или у человека имеется дальнозоркость или близорукость.

е) Познай самого себя.

ж) Не может быть, что ни один человек не дышит жабрами.

з) Талант всегда пробьет себе дорогу.

и) Некоторые животные мыслят.

к) Информатика, в частности, изучает алгоритмы.

л) Всякая истина является конкретной.

м) Это утверждение ложно.

8. Определите формы следующих сложных высказываний, записав их на языке алгебр логики:

а) Чтобы погода была солнечной, достаточно, чтобы не было ни ветра, ни дождя.

б) Если у меня будет свободное время и не будет дождя, то я не буду решать задачи по математике, а пойду на дискотеку.

в) Лошадь погибает от одного грамма никотина, но я не лошадь, следовательно, курить вредно.

г) Без Вас хочу сказать Вам много,

При Вас я слушать Вас хочу.

д) Люди получают высшее образование тогда, когда они заканчивают институт, университет или академию.

9. Постройте таблицы истинности следующих сложных высказываний и определите, являются ли эти высказывания тождественно истинными:

а)

б)

в)

г)

д)

10. Определите, какие из следующих пар высказываний являются эквивалентными, а какие нет:

а)

б)

в)

г)

д)

е)

ж)

з)

и)

к)

л)

м)

11. Проверьте следующие равносильности двумя способами: построив таблицу истинности и упростив левую и правую части равенства.

а)

б)

в)

12. Упростите следующие выражения:

а)

б)

в)

г)

д)

Используя алгебру высказываний, решить логическую содержательную задачу:

 

13. Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:

Алеша. Этот сосуд греческий и изготовлен в V веке.

Боря. Это сосуд финикийский и изготовлен в III веке.

Гриша. Этот сосуд не греческий и изготовлен в IV веке.

Археолог сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?

 

14. В одном королевстве были незамужние принцессы, голодные тигры и приговоренный к казни узник. Но король всякому узнику, осужденному на смерть, давал последний шанс спастись. Ему предлагалось угадать, в какой из двух комнат находятся тигр, а в какой принцесса. Хотя вполне могло быть, что король в обеих комнатах разместил принцесс или, что могло быть хуже, в обеих тигров. Выбор надо было сделать на основании табличек на дверях комнат. Причем, узнику было известно, что утверждения на табличках либо оба истинны, либо оба ложны. Надписи гласили:

Первая комната:	Вторая комната:
По крайней мере в одной из комнат находится принцесса	Тигр в другой комнате

Какую дверь должен выбрать узник?

 

15. На соревнованиях по легкой атлетике Андрей, Боря, Сережа и Володя заняли первые четыре места. Но когда девочки стали вспоминать, как эти места распределились между победителями, то мнения разошлись:

Даша: Андрей был первым, а Володя – вторым.

Галя: Андрей был вторым, а Борис – третьим.

Лена: Боря был четвертым, а Сережа – вторым.

Ася, которая была судьей на этих соревнованиях и хорошо помнила, как распределились места, сказала, что каждая из девочек сделала одно правильное и одно неправильное заявление. Кто из ребят какое место занял?

 

16. В одной стране жили рыцари, которые всегда говорили только правду, и лжецы, которые всегда лгали. Однажды в страну проник шпион по имени Мердок, который, как и всякий шпион, иногда говорил правду, иногда лгал, в зависимости от того, что ему выгодно. Шпион поселился с двумя жителями страны – рыцарем и лжецом. Всех троих арестовали в один день и привели на допрос. Никто не знал, кто из них – кто. Они сделали следующие заявления:

А сказал: Я – Мердок.

В сказал: А говорит правду.

С сказал: Я не Мердок.

Кто же из них шпион – А, В или С?