Определение шагов варьирования факторов
Определение шагов движения к экстремуму методом крутого восхождения. Один из факторов Хi принимают за базовый и для него вычисляют произведение соответствующего коэффициента регрессии bi на шаг варьирования dхi. Например, для первого фактора Х1 это произведение имеет вид (b1 · х1). Затем для базового фактора Х1 выбирают шаг движения ∆х1*, с которым будет осуществляться оптимизация. Шаг движения выбирается произвольно, однако он должен быть меньше интервала варьирования dх1. При этом необходимо помнить, что небольшой шаг – увеличит число опытов при движении к оптимуму, а большой шаг движения увеличивает вероятность проскочить область оптимума. Поэтому рекомендуется учитывать нижнюю границу, которая задается возможностью фиксирования двух соседних опытов, и верхнюю, которая ограничивается областью определения факторов. После этого вычислить шаг движения g по формуле 17: g = ∆х1*/ b1 · dх1 (17) Для всех остальных факторов шаги движения к оптимальным значениям рассчитывают по формуле 18: ∆хi*= g · bi · dхi (18) Если какой-то фактор имеет ограничения, то его стабилизируют на максимально (минимально) возможном уровне, а другие продолжают изменять с тем же шагом. Если же ищется минимум функции у, то новые значения факторов находят из предыдущих путем вычитания ∆хi*. Такой способ оптимизации называют методом наискорейшего спуска. Если есть подозрение, что существует несколько оптимумов, то рекомендуется начинать движение от разных исходных точек, располагаемых в разных областях факторного пространства. При оптимизации симплексным методом иопределении шагов движения к экстремуму необходимо принимать во внимание ограничения, наложенные на влияющие факторы и функции отклика. Матрица опытов исходного симплекса в кодированных переменных приведена в табл. 2. Символом «0» (ноль) обозначены координаты центра плана, т. е. основной уровень. Таблица 2. Матрица исходного симплекса
Величины, входящие в эту таблицу, рассчитывают по следующим формулам19 и 20:
Ri = i ki (20) где i— номер фактора в матрице планирования, п – число факторов. Опыты, представленные в табл. 2, соответствуют вершинам симплекса, сторона которого равна единице, а центр совпадает с началом координат (в кодированных переменных). Условия проведения начальной серии опытов, рассчитали по формулам 19 и 20, представили в таблице 3. Таблица 3. Условия начальной серии опытов
Аналогично можно рассчитать условия исходной серии опытов для любого количества факторов. Если исследуется влияние трех факторов, то для расчета начальных условий опытов следует взять из таблицы 3 данные трех столбцов и четырех строк.
2.3.2. Оптимизация поверхности отклика математической модели Движение к оптимуму методом крутого восхождения начинают из центра плана, который использовался для получения математического описания функции отклика. Значения факторов на каждом новом шаге находят путем прибавления к соответствующим предыдущим значениям. Центр плана для кодированных переменных также можно рассчитать из формулы (1) с использованием физических переменных Х1, Х2, Х3 и шагов варьирования, принятых ранее в полном факторном эксперименте.
хi = (Хi - Хoi) / ∆ Хi (21) где i = 1, 2, …, n; ∆ Хi – шаг варьирования или масштаб по оси Хi; Хi0 – центр варьирования переменных; хi - называют кодированной переменной. Двигаясь по градиенту от центра плана на шаг движения, путем последовательного прибавления значения шага для каждого фактора, определим условия опытов крутого восхождения. Эти опыты часто называют мысленными. Подставляя полученные кодированные переменные в уравнение регрессии получим расчетные значения ур параметра оптимизации в зависимости от условий опытов Х1, Х2, Х3 и т.д. Значения кодированных переменных берутся по модулю | Х 1|, | Х 2 | и| Х 3|, так как знак в данном случае указывает на направление движения. Значения уэ взятьиз пункта 2.4 или таблицы МП. Результаты представить в виде таблицы 4.
Таблица 4. Результаты опытов по методу крутого восхождения
Примечание: у1р и у1э - соответственно расчетные и экспериментальные значения параметра оптимизации.
Движение к оптимуму прекратить в следующих случаях: 1. Значение (одного или нескольких) факторов или функций отклика вышли за границы допустимых значений. 2. Достигнут экстремум критерия оптимальности у. В первом случае на этом оптимизация заканчивается. Во втором случае в области экстремума функции у ищут ее новое математическое описание, используя полный факторный эксперимент или метод дробных реплик. Опытным путем подтверждаются значения ур,полученные с помощью ПФЭ и оптимизации градиентным методом крутого восхождения.
Оптимизация поверхности отклика симплексным методом. Условия каждого нового опыта рассчитать по формуле 22:
где п – число факторов в матрице планирования, i— номер фактора, j –номер опыта, xi* - значение i –го фактора в самом «неудачном» опыте предыдущего симплекса. Симплексный метод оптимизации позволяет на любом шаге нахождения экстремума включит в программу новый фактор, который до этого был на постоянном уровне и не принимался во внимание. При этом количество опытов увеличивается вдвое. Значения всех, ранее рассмотренных факторов, рассчитать по формуле 23:
где i=1, 2,.., п - является средним арифметическим значением соответствующих координат предыдущего симплекса. Значение вновь вводимого фактора определить по формуле 24:
Хп+1 = Хo(п+1) + ∆ Хп+1 (Rп+1 + k п+1) (24) где Хo(п+1) – основной уровень этого фактора; ∆ Хп+1 – выбранный шаг варьирования для данного фактора; Rп+1 и k п+1 - величины, рассчитанные по формулам 19 и 20. Результаты оптимизации по симплексному методу представить в виде таблицы 5. Исключая неудачные опыты и заменяя их новыми, приближаемся к экстремуму. Движение продолжается до тех пор, пока зеркальная точка нового симплекса является его наихудшей вершиной, т.е. поступательное перемещение симплекса преобразуется в качание относительно противолежащей грани, что может свидетельствовать о приближении к экстремуму поверхности отклика. Таблица 5. Условия и результаты планирования по симплексному методу
Пока точка экстремума в факторном пространстве остается неподвижной, симплекс постоянно качается, вращается около некоторой близкой к ней точки. Если же точка экстремума начинает дрейфовать, то вслед за ней перемещается и симплекс, описывая спираль около ее траектории. При этом условия управления объектом будут непрерывно изменяться, приспосабливаясь к Дрейфу.
|

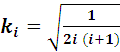 (19)
(19)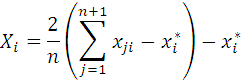 (22)
(22)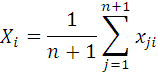 (23)
(23)


