Проверка адекватности полученной модели
После получения уравнения производится статистический анализ значимости вычисленных коэффициентов и проверка адекватности уравнения регрессии. С этой целью вычисляют построчные дисперсии в каждом опыте плана, характеризующие изменчивость результатов в опытах плана относительно их средних значений. Вычислить критерии адекватности и погрешности эксперимента по формулам 12 и 13: -дисперсия воспроизводимости параллельных опытов характеризует погрешность наблюдений: - проверка адекватности воспроизводимости:
Извлекая корень, вычислить дисперсию коэффициентов регрессии S b. Статистическую значимость коэффициентов регрессии проверить по критерию Стьюдента t. Коэффициенты регрессии значимы, если |b|≥ S b t. Рассчитать критерий Стьюдента для всех коэффициентов регрессии по формуле 14: tр = |bi| / S b (14) Для доверительной вероятности Р=0,95, при числе степеней свободы f=N(т -1), табличное значение критерия Стьюдента взять из приложения 5. Отбросив все статистически незначимые коэффициенты, получили математическое описание процесса в виде линейного уравнения регрессии. Уравнение, включающее только оставшиеся значимые коэффициенты, проверить на адекватность. Проверку адекватности уравнения регрессии исследуемого объекта провести по критерию Фишера (формула 15).
где Для оценки дисперсии адекватности необходимо оценить, насколько отличаются средние значения экспериментального ỹiэ выходного параметра, полученного в точках факторного пространства, и значения расчетного yiр, полученного из уравнения регрессии в тех же точках факторного пространства. Вычислить оценку дисперсности адекватности по формуле 16:
где N - общее число опытов ПФЭ; В- число коэффициентов регрессии искомого уравнения; уjэ, уjр - экспериментальное и расчетное значение функции отклика в j-м опыте. Определить расчетное значение ỹiр, подставляя в уравнение регрессии вместо Х1, Х2, …, знаки (+1) или (-1), в соответсвии с матрицей планирования эксперимента. Произвести расчет F- критерия Фишера по формуле 15: Fp = S2 ад / S2 воспр Найденное расчетным путем Fp сравнивают с табличным значением критерия Фишера Fтабл, которое определяется при уровне значимости a=0,05 и числе степеней свободы fад(1)=(N – В) и fв(2) = N(m - 1) из приложения 6. Если Fp< Fтабл, то полученная математическая модель с принятым уровнем статистической значимости a=0,05 адекватна экспериментальным данным. Следовательно, полученное вами уравнение регрессии является адекватным исследуемому объекту, при доверительной вероятности Р=0,95, и позволяет оптимизировать процесс производства или качество исследуемого объекта. При превышении табличного значения эта гипотеза отвергается, а уравнение считается неадекватным. Если линейная модель неадекватна, значит, не удается аппроксимировать поверхность отклика плоскостью. В этом случае рекомендуется применить другой метод планирования эксперимента.
|

 , (12)
, (12) (13)
(13) , (15)
, (15) – оценка дисперсии адекватности,
– оценка дисперсии адекватности, 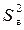 - дисперсия воспроизводимости.
- дисперсия воспроизводимости. , (16)
, (16)


