Погрешности метода решения
Рассмотрим более подробно погрешности, возникающие при решении задачи Коши приближенными методами. Эти погрешности называют ошибками метода решения или ошибками дискретизации. Локальная ошибка – ошибка, сделанная на одном шаге приращения аргумента, при условии, что предыдущие значения точны. Обозначим: un(t) – точное решение уравнения
Глобальная ошибка дискретизации равна
Глобальная ошибка – это ошибка, накопленная за n шагов. В общем случае глобальная ошибка может быть как больше, так и меньше суммы локальных. На рис. 8.4 показаны глобальные и локальные ошибки в случае решения методом Эйлера начальной задачи:
Точное решение этой задачи представляет собой экспоненциальную функцию:
Если изменить знак коэффициента  , получим затухающее решение. В этом случае будет справедливо обратное соотношение: , получим затухающее решение. В этом случае будет справедливо обратное соотношение: 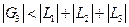 . .
В частном случае вырожденного дифференциального уравнения
Определение. Метод имеет порядок p, если существует положительное число
Число C зависит от производных функции Неравенство может быть записано более компактно:
Порядок метода Эйлера равен p=1, так что уменьшение средней длины шага в 2 раза уменьшит среднюю локальную ошибку в 4 раза. Но на том же отрезке интегрирования уравнения потребуется приблизительно вдвое больше шагов. Поэтому глобальная ошибка уменьшится лишь примерно в два раза.
|

 при условии
при условии  . Как и прежде yn обозначает приближенное решение уравнения в точке tn. Локальная ошибка, сделанная на n-ом шаге, равна
. Как и прежде yn обозначает приближенное решение уравнения в точке tn. Локальная ошибка, сделанная на n-ом шаге, равна . (8.13)
. (8.13) . (8.14)
. (8.14) .
.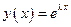 . Это точное решение показано на рисунке верхней линией. Нижняя ломаная линия представляет собой ломаную Эйлера. Видно, что в данном случае глобальная погрешность больше суммы локальных:
. Это точное решение показано на рисунке верхней линией. Нижняя ломаная линия представляет собой ломаную Эйлера. Видно, что в данном случае глобальная погрешность больше суммы локальных:  .
.
 , у которого правая часть уравнения не зависит от y, глобальная ошибка равна сумме локальных:
, у которого правая часть уравнения не зависит от y, глобальная ошибка равна сумме локальных: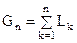 .
. такое, что
такое, что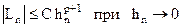 . (8.15)
. (8.15) , определяющей правую часть дифференциального уравнения, и может зависеть также от длины интервала, на котором ищется решение. Но это число не должно зависеть от номера шага n и величины шага hn.
, определяющей правую часть дифференциального уравнения, и может зависеть также от длины интервала, на котором ищется решение. Но это число не должно зависеть от номера шага n и величины шага hn. . (8.16)
. (8.16)


