Модифицированные методы Эйлера
Представим точное решение дифференциального уравнения
Запишем приближенное решение в виде:
Подберем такую функцию Ф, чтобы
где Разложим функцию Ф в ряд по степеням h:
где по-прежнему Из сравнения (8.17) и (8.19) с учетом (8.18) следует, что коэффициенты
1) Положив
Произведение, стоящее в правой части формулы (8.21), имеет вид формулы прямоугольников для вычисления интегралов (см. рис. 8.2). Отличие от квадратурной формулы прямоугольников состоит в том, что нам неизвестно точное значение функции f в середине отрезка интегрирования 2) Положив
Произведение, стоящее в правой части формулы (8.22), похоже на квадратурную формулу трапеций. Отличие от формулы трапеций состоит в том, что нам неизвестно точное значение функции f в точке
Пример 8.6. Найдем решение начальной задачи:
двумя методами: методом Эйлера и вторым модифицированным методом Эйлера. Проведем только один шаг решения, т.е. найдем Точное решение легко может быть найдено аналитически, либо может быть найдено в среде Mathematica выполнением команды: In[]:= DSolve[ {y'[x]==x+y[x], y[1]==1}, y[x], x]//Expand Точное решение равно: Решение методом Эйлера: Решение вторым модифицированным методом Эйлера:
Видим, что решение модифицированным методом ближе к точному решению. Пример 8.7. Найдем решение начальной задачи:
В примере 8.2 эта задача решена методом Эйлера. Получены значения:
Найдем теперь решение первым модифицированным методом. Проведем только один шаг решения, т.е. найдем
Видим, что решение модифицированным методом существенно точнее, чем решение простым методом Эйлера.
|

 , проходящее через точку
, проходящее через точку  , в виде ряда Тейлора:
, в виде ряда Тейлора: (8.17)
(8.17) (8.18)
(8.18) было равно сумме первых трех слагаемых в формуле (8.17). Будем искать функцию Ф в виде:
было равно сумме первых трех слагаемых в формуле (8.17). Будем искать функцию Ф в виде: ,
, – пока неизвестные коэффициенты.
– пока неизвестные коэффициенты. (8.19)
(8.19) .
. (8.20)
(8.20) , т.е.
, т.е. 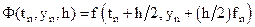 , получим первый модифицированный метод Эйлера:
, получим первый модифицированный метод Эйлера: (8.21)
(8.21)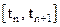 .
. , т.е.
, т.е.  , получим второй модифицированный метод Эйлера:
, получим второй модифицированный метод Эйлера: (8.22)
(8.22) .
.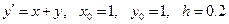 , –
, – . Сравним результаты вычислений с точным решением.
. Сравним результаты вычислений с точным решением. и
и  .
. .
. .
. .
. . Точное решение этой задачи равно:
. Точное решение этой задачи равно:
 .
. .
. .
.


