Методы Рунге-Кутта
При использовании методов Рунге-Кутта для решения уравнения
..............., (8.25)
Значение неизвестной функции в новой точке вычисляется по формуле:
Простейшим примером является второй модифицированный метод Эйлера, который может быть описан следующей последовательностью формул:
Для построения метода Рунге-Кутта требуемого порядка нужно найти коэффициенты Обозначим: u(x) – точное решение, проходящее через точку (x, y(x)). Тогда
если f(x,y) – произвольная достаточно гладкая функция, и найдется такая гладкая функция f(x,y), что
Итак, если выполнены соотношения (8.26), то метод имеет порядок p. Следовательно, чтобы построить метод порядка p, нужно найти такие коэффициенты In[]:= y'[x_]=f[x, y[x]]; Table[{k," ", D[f[x, y[x]], {x, k}]//Expand}, {k, 1, 3}]
Для получения метода третьего порядка необходимо взять q=3. Получается система из шести уравнений с восемью неизвестными. Наиболее употребительная совокупность формул для метода третьего порядка:
Можно усмотреть здесь аналогию с квадратурной формулой Симпсона. Наиболее употребительный вариант метода Рунге-Кутта четвертого порядка может быть описан последовательностью формул:
В системе Mathcad встроенная функция, реализующая метод Рунге-Кутта четвертого порядка, для решения системы из n уравнений, вызывается командой: rkfixed(y, x1, x2, npoints, D). Аргументы функции: · y – вектор, содержащий n начальных условий, · x1, x2 – начальная и конечная точки отрезка интегрирования, · npoints – количество точек, в которых вычисляется приближенное решение, · D – вектор, размерности n, содержащий правые части системы уравнений. В случае одного уравнения y и D – скалярные величины. Функция rkfixed применяется также для решения уравнения n-го порядка, которое может быть нелинейным относительно старшей производной. В этом случае уравнение предварительно преобразуется к системе уравнений первого порядка. Функция rkfixed возвращает матрицу, в которой первый столбец содержит значения независимой переменной, а остальные столбцы содержат найденные значения неизвестных функций. Количество строк возвращаемой матрицы равно npoints+1. Пример 8.9. Сравним погрешности решения начальной задачи
На отрезке Решение методом Рунге-Кутта находим с помощью встроенной функции rkfixed. Аргументы функции: 1 – значение y в начальной точке; 0, 2 – отрезок интегрирования уравнения; N – количество узлов сетки; D – функция, описывающая правую часть дифференциального уравнения, D(t, y)=y. Решение методом Рунге-Кутта и точное решение показаны на правом рисунке. Формируем матрицу погрешностей Err. Первый столбец матрицы включает значения
|

 на каждом шаге приращения аргумента вычисляются значения функции f(x,y) в нескольких точках. Последовательно находятся:
на каждом шаге приращения аргумента вычисляются значения функции f(x,y) в нескольких точках. Последовательно находятся: ,
, .
. .
. ,
, .
. .
. равно локальной погрешности метода. Если f(x,y) – достаточно гладкая функция своих аргументов, то все ki(h), i=1,..,q и
равно локальной погрешности метода. Если f(x,y) – достаточно гладкая функция своих аргументов, то все ki(h), i=1,..,q и  – гладкие функции параметра h. Предположим, что
– гладкие функции параметра h. Предположим, что , (8.26)
, (8.26) . Тогда по формуле Тейлора
. Тогда по формуле Тейлора .
.
 (8.27)
(8.27) (8.28)
(8.28) тремя методами: простым и модифицированным методами Эйлера, а также методом Рунге-Кутта. Решение в среде Mathcad приведено на рис. 8.6. Точное решение задачи представляет собой экспоненциальную функцию
тремя методами: простым и модифицированным методами Эйлера, а также методом Рунге-Кутта. Решение в среде Mathcad приведено на рис. 8.6. Точное решение задачи представляет собой экспоненциальную функцию  .
.
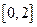 задаем равномерную сетку значений аргумента
задаем равномерную сетку значений аргумента  с шагом
с шагом 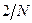 . Последовательность
. Последовательность  включает решение обычным методом Эйлера. Решение первым модифицированным методом Эйлера представляет последовательность
включает решение обычным методом Эйлера. Решение первым модифицированным методом Эйлера представляет последовательность  . На левом графике показаны эти два решения и точное решение
. На левом графике показаны эти два решения и точное решение  .
.


