Как и прежде рассматриваем задачу Коши:
 .
.
Неявный метод Эйлера описывается формулой:
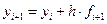 , (8.11)
, (8.11)
где  . Как видим, в отличие от обычного, явного метода Эйлера искомая величина
. Как видим, в отличие от обычного, явного метода Эйлера искомая величина  входит также и в правую часть уравнения (8.11). Поэтому на каждом шаге приращения аргумента необходимо решать уравнение относительно
входит также и в правую часть уравнения (8.11). Поэтому на каждом шаге приращения аргумента необходимо решать уравнение относительно  . Достоинством неявного метода Эйлера является то, что он устойчив при любом выборе шага приращения аргумента.
. Достоинством неявного метода Эйлера является то, что он устойчив при любом выборе шага приращения аргумента.
Неявный метод Эйлера может быть получен из интегрального уравнения (8.5):
 , –
, –
если подынтегральную функцию заменить константой  .
.
Пример 8.10. Найдем решение начальной задачи:
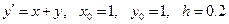 , –
, –
неявным методом Эйлера.
Неявный метод для данного уравнения описывается формулой:
 .
.
Отсюда
 и
и 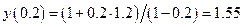 .
.
Пример 8.11. Найдем неявным методом Эйлера решение начальной задачи:
 .
.
В примере 8.2 эта задача была решена явным методом Эйлера. Неявный метод описывается формулами:
 или
или 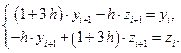
Решив эту систему линейных алгебраических уравнений, получим:
 (8.12)
(8.12)

Решение в среде Mathcad на отрезке 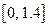 показано на рис. 8.6. Итерационный процесс в соответствии с формулами (8.12) записан в векторной форме. Шаг приращения аргумента полагается равным
показано на рис. 8.6. Итерационный процесс в соответствии с формулами (8.12) записан в векторной форме. Шаг приращения аргумента полагается равным  , где
, где  – число точек на отрезке интегрирования. Окончательная матрица
– число точек на отрезке интегрирования. Окончательная матрица 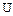 содержит в первой строке значения
содержит в первой строке значения  , во второй и третьей строках – приближенные значения
, во второй и третьей строках – приближенные значения  и
и  , в четвертой и пятой строках – точные решения
, в четвертой и пятой строках – точные решения  .
.
Из сравнения с рис.8.2 видим, что неявный метод для данной задачи оказывается более точным.

 .
.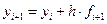 , (8.11)
, (8.11) . Как видим, в отличие от обычного, явного метода Эйлера искомая величина
. Как видим, в отличие от обычного, явного метода Эйлера искомая величина  входит также и в правую часть уравнения (8.11). Поэтому на каждом шаге приращения аргумента необходимо решать уравнение относительно
входит также и в правую часть уравнения (8.11). Поэтому на каждом шаге приращения аргумента необходимо решать уравнение относительно  , –
, – .
.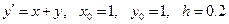 , –
, – .
. и
и 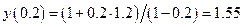 .
. .
. или
или 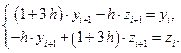
 (8.12)
(8.12)
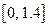 показано на рис. 8.6. Итерационный процесс в соответствии с формулами (8.12) записан в векторной форме. Шаг приращения аргумента полагается равным
показано на рис. 8.6. Итерационный процесс в соответствии с формулами (8.12) записан в векторной форме. Шаг приращения аргумента полагается равным  , где
, где  – число точек на отрезке интегрирования. Окончательная матрица
– число точек на отрезке интегрирования. Окончательная матрица 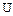 содержит в первой строке значения
содержит в первой строке значения  , во второй и третьей строках – приближенные значения
, во второй и третьей строках – приближенные значения  и
и  , в четвертой и пятой строках – точные решения
, в четвертой и пятой строках – точные решения  .
.


