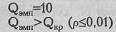Решение задачи 2
Поскольку в обеих выборках n 1, n 2>11 и диапазоны разброса значений в двух выборках не совпадают между собой, мы можем воспользоваться самым простым критерием для сопоставления двух выборок -критерием Q Розенбаума. Объемы выборок различаются менее чем на 10 человек, так что ограничение о примерном равенстве выборок также не препятствует нам. Данные в Табл. 2.10 уже упорядочены по возрастанию признака. Первым, более высоким, рядом является ряд значений в мужской выборке. Средняя величина тоже выше в выборке мужчин. Сформулируем гипотезы. H0: При обращении в службу знакомств мужчинам приходится преодолевать не более интенсивное внутреннее сопротивление, чем женщинам. H1: При обращении в службу знакомств мужчинам приходится преодолевать более интенсивное внутреннее сопротивление, чем женщинам. Сопоставим ряды значений для определения S1 и S2. В Табл. 9.2 отмечены два интересующих нас значения: максимальное значение 2-го ряда (max 2) и минимальное значение 1-го ряда (min 1). Определим S1, как количество значений 1-го ряда, которые превышают максимальное значение 2-го ряда: S1=5. Определяем S2, как количество значений 2-го ряда, которые меньше минимального значения 1-го ряда: S2=5. Вычисляем эмпирическое значение Q как суммы S1 и S2: Q=S1+S2=5+5=10 По Табл. I Приложения 1 определяем критические значения Q при n 1=17, n 2=23:
Таблица 9.2 Расчет критерия Q при сопоставлении мужской (n 1=17) и женской (n 2=23) выборок по показателю интенсивности внутреннего сопротивления при обращении в службу знакомств
Ответ: H0 отвергается. Принимается H1. При обращении в службу знакомств мужчинам из исследованной выборки пришлось преодолеть более мощное внутреннее сопротивление, чем женщинам.
|

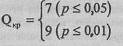
 81
81
 25
25