Односторонние пределы. В определении предела функции =А считается, что х стремится к хо любым способом: оставаясь меньшим
В определении предела функции Бывают случаи, когда способ приближения аргумента х к хо существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов. Число А1 называется пределом функции у = f(х) слева в точке хо, если для любого число ε>0 существует число δ = δ (ε) > О такое, что при х Î (хо — δ; хо), выполняется неравенство ½f(х) — А1 ½< ε. Предел слева записывают так:
Аналогично определяется предел функции справа, запишем его с помощью символов:
Коротко предел справа обозначают f(хо + 0) = А2. Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует Если же А1 ≠А2, то Предел функции при х →∞; Пусть функция у = f(х) определена в промежутке (—∞; ∞). Число А называется пределом функции f(х) при х →∞, если для любого положительного числа ε существует такое число М = М(ε) > О, что при всех х, удовлетворяющих неравенству ½х½ > М выполняется неравенство ½f(х) — А½< ε. Коротко это определение можно записать так:
Если х →+∞, то пишут А= Геометрический смысл этого определения таков: для " ε>0 $М>0, что при хÎ(-∞;М) или хÎ(М;+ ∞) соответствующие значения функции f(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у =А+ε и у =А—ε (см. рис.)
|

 =А считается, что х стремится к хо любым способом: оставаясь меньшим, чем хо (слева от хо), большим, чем хо (справа от хо), или колеблясь около точки хо.
=А считается, что х стремится к хо любым способом: оставаясь меньшим, чем хо (слева от хо), большим, чем хо (справа от хо), или колеблясь около точки хо. =А1 или коротко: f(х0-0)=А1 (обозначение Дирихле).
=А1 или коротко: f(х0-0)=А1 (обозначение Дирихле).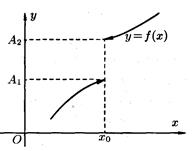


 , если х →+∞, то — А =
, если х →+∞, то — А = 




