Геометрический смысл дифференциала
Из рисунка видно, что при Δ х →0 М1 стремится к М и разность между приращением функции М1N и дифференциалом функции КN стремится к нулю. Это дает основание использования дифференциала для приближенных вычислений: 1). 2). Пример. Вычислить приближенно Получим сначала приближенную формулу для вычисления корней любого Или В данном примере
Возьмем за число близкое до 16,64 и такое, чтобы мы знали при этом Δ х должно быть достаточно малым. Понятно, что в нашем случае нужно взять
Кроме того, с помощью дифференциала может быть решена задача об определении абсолютной и относительной погрешности вычисления функции при заданной погрешности измерения аргумента. Мы ввели понятие дифференциала для функции у = f(х). пусть теперь у=f(u), где аргумент u=φ(х), то есть у является сложной функцией у=f(φ(х)). Если у=f(u) и u=φ(х) - дифференцируемые функции, то мы знаем, что
потому, что Последнее равенство показывает, что форма дифференциала не зависит от того, будет ли функция простой, или сложной. Это свойство носит название инвариантности формы первого дифференциала. Следует понимать при этом, что инвариантна только форма. Содержание же различно, так как в формуле (5.18) Дифференциал функции Дифференциалом второго порядка при этом Аналогично можно ввести понятие дифференциала Ш, ІV и так далее порядков. Определение. Дифференциалом
Обратим внимание на то, что, если
|


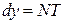 - дифференциал: это приращение ординаты точки, движущейся по касательной к кривой.
- дифференциал: это приращение ординаты точки, движущейся по касательной к кривой. ;
;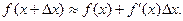 (5.20)
(5.20)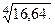
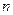 - й степени. Поскольку
- й степени. Поскольку 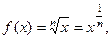 то
то 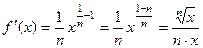 . И соответственно (5.20)
. И соответственно (5.20)  ,
,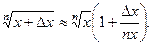 (5.21)
(5.21)
 ,
,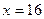 , тогда
, тогда  и мы получим
и мы получим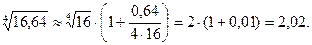
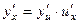 . Тогда дифференциал этой функции
. Тогда дифференциал этой функции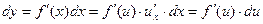 ,
, . Т.о.
. Т.о. 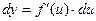 . (5.22)
. (5.22)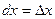 , а в формуле (5.22)
, а в формуле (5.22)  .
. , вычисленный по формуле (5.18), называют еще дифференциалом первого порядка. Он представляет собой некоторую функцию от
, вычисленный по формуле (5.18), называют еще дифференциалом первого порядка. Он представляет собой некоторую функцию от  , которая также может иметь дифференциал.
, которая также может иметь дифференциал. дважды дифференцируемой на
дважды дифференцируемой на  функции у= f(х) называется дифференциал от дифференциала первого порядка этой функции, то есть
функции у= f(х) называется дифференциал от дифференциала первого порядка этой функции, то есть 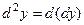 ,
, . (5.23)
. (5.23)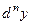 для
для 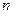 раз дифференцируемой на
раз дифференцируемой на 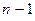 ) - го порядка данной функции, т.е.
) - го порядка данной функции, т.е. 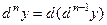 .
. . (5.24)
. (5.24)
 .
.


