СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
I. 1) область определения; 2) область значений; 3) наличие точек разрыва и их характер; определить невертикальные (наклонные и горизонтальные) асимптоты; 4) четность, нечетность (указать характер поведения графика функции); 5) периодичность; 6) нули (указать точки пересечения с осями координат).
II. Интервалы монотонности и экстремумы 1) определить интервалы монотонности; 2) определить критические точки І рода и значения функции в них; 3) указать точки экстремума. III. Промежутки выпуклости и точки перегиба 1) определить промежутки выпуклости графика; 2) определить точки перегиба и значения функции в них. ІV. Внести данные в таблицы.
V. Построить график функции в декартовой системе координат. Пример 5. Дана функция Решение: Продифференцировать левую и праву части, учитывая, что
Решим данное уравнение относительно
Пример 6. Найти производную функции, заданной уравнением: Решение:
Пример 7. Найти уравнение касательной и нормали к кривой Решение: Уравнение касательной:
Уравнение касательной: Уравнение нормали:
Пример 8. Найти Решение:
Пример 9. Вычислить Решение: Имеем неопределенность вида
Пример 10. Вычислить Решение: Имеем неопределенность вида
Пример 11. Исследовать функцию Решение: 1. Область определения: 2. Функция имеет разрывы при 3. Ведь
|

 . Найти
. Найти  .
. является функцией от
является функцией от  .
. .
. .
.
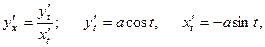 тогда
тогда 
 в точке
в точке  .
. .
.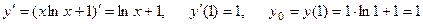 .
. .
. ,
, - уравнение нормали.
- уравнение нормали.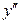 , если
, если 


 . Воспользовавшись правилом Лопиталя, получим:
. Воспользовавшись правилом Лопиталя, получим:
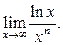
 . Воспользовавшись правилом Лопиталя, получим:
. Воспользовавшись правилом Лопиталя, получим: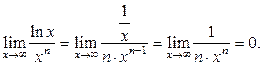
 и построить ее график.
и построить ее график.


 - вертикальная асимптота.
- вертикальная асимптота.


