Производная функции
При изучении различных материальных процессов, например движения тела, течения химических реакций, экономических процессов (спроса и затрат), мы встречаемся с задачей определения скорости изменения соответствующих величин. В большинстве случаев такие задачи не могут быть решены с помощью элементарной математики. Для их решения пользуются дифференциальным исчислением. Итак, рассмотрим более детально задачу о прямолинейном движении некоторого твердого тела. Предположим, что между пройденным телом путем и временами, за который пройден этот путь, существует зависимость S = f(t). (5.1) Предположим также, что движение началось в т.0 при t=0 (рис.1).
За время t тело прошло путь S = f(t) и оказалось в точке А, а в следующий момент времени t+Δt оно оказалось в точке В. Обозначим путь, который прошло тело за время t+Δt, через S1. Итак, за время Δt тело прошло путь S1-S= f(t+ Δt) - f(t) Тогда средняя скорость движения тела на отрезке АВ будет определяться по формуле (5.2)
Но эта скорость не будет мгновенной скоростью в момент t. Если говорят, например, что поезд двигается со скоростью 100 км/ч, то это не означает, что он имеет такую скорость все время, понятно, что в начале движения и в конце его скорость меньше. Чем меньше промежуток времени, на котором измеряется средняя скорость, тем ближе результат измерения к фактической скорости в момент времени t. Итак, мгновенная скорость тела в момент времени t будет равна К такому же результату мы придем, если будем определять скорость химической реакции, скорость выпаривания вещества и т.п. Итак, разные с физической точки зрения задачи приводят к необходимости выполнения одинаковых с математической точки зрения действий, а именно, вычисления предела отношения приращения функции к приращению аргумента при условии, что последний стремится к нулю. Приращением функции f(х) в точке х0 называется разность между значением функции в точке
Определение: производной функции у=f(х) в точке х называется предел отношения приращения функции Δу в точке х к приращению аргумента Δх, при условии, что приращение аргумента стремится к нулю Дифференцирование функции f(х) - это операция нахождения ее производной.
|


 . (5.2)
. (5.2) . (5.3)
. (5.3) и ее значением в точке х0
и ее значением в точке х0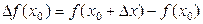 .
. .
.


