Пусть функция у = f(х) определена и имеет производную первого порядка в интервале  . Введем обозначение
. Введем обозначение  . Если функция
. Если функция  имеет производную в точке
имеет производную в точке  , то ее производная
, то ее производная  называется производной второго порядка (или коротко второй производной) функции
называется производной второго порядка (или коротко второй производной) функции  в точке
в точке  . Итак,
. Итак,
 .
.
Вторая производная функции у = f(х) обозначается символами
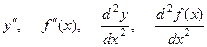 .
.
Может оказаться, что вторая производная также имеет производную в точке  :
:  .
.
Тогда говорят о существовании производной третьего порядка, которая обозначается символами  .
.
Предположим, что таким образом определена производная  - го порядка
- го порядка  .
.
Определение 4. Производная 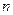 - го порядка (
- го порядка (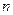 - ая производная) функции у = f(х) называется производная от производной (
- ая производная) функции у = f(х) называется производная от производной ( ) - го порядка, если она существует в точке
) - го порядка, если она существует в точке  . Производную
. Производную 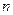 - го порядка
- го порядка 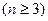 функции у = f(х) обозначают символами:
функции у = f(х) обозначают символами:
 .
.
В соответствии с этим обозначением 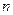 - производная функции
- производная функции  определяется равенством
определяется равенством 
Пример. Функция  имеет в каждой точке производную
имеет в каждой точке производную  . Функция
. Функция  также в каждой точке имеет производную
также в каждой точке имеет производную  . Функция
. Функция  в каждой точке имеет производную
в каждой точке имеет производную  Функция
Функция  имеет в каждой точке производную
имеет в каждой точке производную  Все другие следующие производные также равны 0.
Все другие следующие производные также равны 0.
Итак,
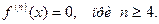
Производные высших порядков имеют широкое применение. Так, если  описывает закон движения материальной точки, то его первая производная
описывает закон движения материальной точки, то его первая производная 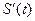 определяет величину мгновенной скорости, а вторая производная
определяет величину мгновенной скорости, а вторая производная  равна скорости изменения скорости, то есть ускорению в момент
равна скорости изменения скорости, то есть ускорению в момент  .
.

 . Введем обозначение
. Введем обозначение  . Если функция
. Если функция  имеет производную в точке
имеет производную в точке  , то ее производная
, то ее производная  называется производной второго порядка (или коротко второй производной) функции
называется производной второго порядка (или коротко второй производной) функции  в точке
в точке  . Итак,
. Итак, .
.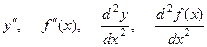 .
. .
. .
. - го порядка
- го порядка  .
.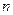 - го порядка (
- го порядка ( ) - го порядка, если она существует в точке
) - го порядка, если она существует в точке 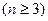 функции у = f(х) обозначают символами:
функции у = f(х) обозначают символами: .
. определяется равенством
определяется равенством 
 имеет в каждой точке производную
имеет в каждой точке производную  . Функция
. Функция  также в каждой точке имеет производную
также в каждой точке имеет производную  . Функция
. Функция  в каждой точке имеет производную
в каждой точке имеет производную  Функция
Функция  имеет в каждой точке производную
имеет в каждой точке производную  Все другие следующие производные также равны 0.
Все другие следующие производные также равны 0.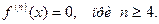
 описывает закон движения материальной точки, то его первая производная
описывает закон движения материальной точки, то его первая производная 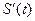 определяет величину мгновенной скорости, а вторая производная
определяет величину мгновенной скорости, а вторая производная  равна скорости изменения скорости, то есть ускорению в момент
равна скорости изменения скорости, то есть ускорению в момент  .
.


