Несмотря на простоту вывода основного уравнения молекулярно-кинетической теории газов, формулу  не так-то просто проверить на опыте. Да, мы умеем измерять на опыте давление газа, но у нас нет приборов для прямого измерения величины энергии Е = Е 1× n. Человечество вообще не умеет измерять внутреннюю энергию газа в состоянии теплового равновесия. Чтобы реально использовать уравнение кинетической теории газов, приходится прибегать к процедуре косвенных измерений величины Е (энергии). Для этого человечество ввело величину, характеризующую состояние теплового равновесия для любых объектов. Читатель правильно догадался, такой величиной является температура; символ – Т.
не так-то просто проверить на опыте. Да, мы умеем измерять на опыте давление газа, но у нас нет приборов для прямого измерения величины энергии Е = Е 1× n. Человечество вообще не умеет измерять внутреннюю энергию газа в состоянии теплового равновесия. Чтобы реально использовать уравнение кинетической теории газов, приходится прибегать к процедуре косвенных измерений величины Е (энергии). Для этого человечество ввело величину, характеризующую состояние теплового равновесия для любых объектов. Читатель правильно догадался, такой величиной является температура; символ – Т.
Пока будем обходиться понятием эмпирической температуры, т.е. той физической величины, которая измеряется на опыте и связана с интуитивным представлением о тепловом равновесии. Эмпирическая температура объекта – это то, что измеряется другим объектом-термометром, приведённым в состояние теплового равновесия с исходным объектом, и служит характеристикой равновесного состояния. В роли такого объекта-термометра может служить любой объект в состоянии теплового равновесия, характеристики которого реагируют на изменение этого состояния.
Из кинетической теории идеального газа следует, давление пропорционально кинетической энергии молекулы (частицы), если объём V, масса газа m и его сортность m неизменны. Вместе с тем из экспериментальных законов Бойля–Мариотта и Гей-Люссака Клапейрону удалось получить уравнение, связывающее все три термодинамических макропараметра вместе; произведение давления и объёма делённое на температуру остаётся постоянным для любого состояния идеального газа 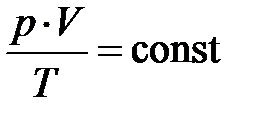 , если сорность и масса газа не изменяются. Эту формулу русский учёный Д.И. Менделееву в 1875 году обобщил для любой массы газа в виде
, если сорность и масса газа не изменяются. Эту формулу русский учёный Д.И. Менделееву в 1875 году обобщил для любой массы газа в виде  , –– объединённый газовый закон. Отсюда следует, при постоянном объёме и массы газа давление пропорционально температуре. Естественно ожидать, температура системы должна быть пропорциональна энергии частицы. Чтобы найти коэффициент пропорциональности между абсолютной температурой Т и энергией частицы Е 1, сопоставим обобщённое уравнение идеального газа и основное уравнение кинетической теории:
, –– объединённый газовый закон. Отсюда следует, при постоянном объёме и массы газа давление пропорционально температуре. Естественно ожидать, температура системы должна быть пропорциональна энергии частицы. Чтобы найти коэффициент пропорциональности между абсолютной температурой Т и энергией частицы Е 1, сопоставим обобщённое уравнение идеального газа и основное уравнение кинетической теории:

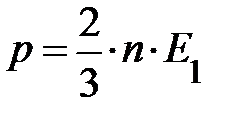 .
.
Если читатель примет к сведению, что m = 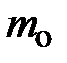 × N,
× N, 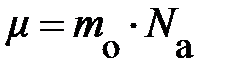 , а
, а  и, проявив терпение, проведёт преобразования первого уравнения, то испытает чувство глубокого удовлетворения, поскольку в результате его действий первое уравнение примет вид
и, проявив терпение, проведёт преобразования первого уравнения, то испытает чувство глубокого удовлетворения, поскольку в результате его действий первое уравнение примет вид  . После преобразований левые части уравнений системы равны, должны быть равны и правые. Отсюда немедленно следует, энергия одной молекулы
. После преобразований левые части уравнений системы равны, должны быть равны и правые. Отсюда немедленно следует, энергия одной молекулы  оказывается зависящей лишь от температуры, но не зависит от массы молекулы; буква k, равная
оказывается зависящей лишь от температуры, но не зависит от массы молекулы; буква k, равная  =
=  , называется постоянной Больцмана. Здесь весьма важно обратить внимание на формулу
, называется постоянной Больцмана. Здесь весьма важно обратить внимание на формулу  . Если имеется смесь из нескольких сортов газов, результирующее давление может быть записано
. Если имеется смесь из нескольких сортов газов, результирующее давление может быть записано 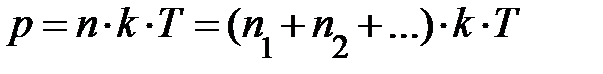 ; здесь
; здесь  – концентрация различных сортов газов. Выражение перепишем
– концентрация различных сортов газов. Выражение перепишем 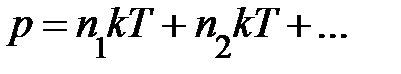 , отсюда немедленно следует закон Дальтона – давление смеси идеальных газов равно сумме парциальных давлений газов, образующих смесь.
, отсюда немедленно следует закон Дальтона – давление смеси идеальных газов равно сумме парциальных давлений газов, образующих смесь.
Следует вернуться к выражению средней энергии молекулы  . При выводе его мы учитывали лишь поступательное движение молекул; здесь «тройка» отражает размерность пространства, в котором происходят рассматриваемые события. Следовательно, на одну степень свободы (возможного направления движения) приходится энергия, равная
. При выводе его мы учитывали лишь поступательное движение молекул; здесь «тройка» отражает размерность пространства, в котором происходят рассматриваемые события. Следовательно, на одну степень свободы (возможного направления движения) приходится энергия, равная  поскольку ни одно из направлений поступательного движения не имеет преимущества. Однако в природе наряду с поступательным движением возможны вращение молекул и колебания атомов в молекуле, входящих в состав молекул. Эти виды движений, также как и поступательное движение, связаны с некоторым запасом энергии, определить который позволяет устанавливаемое статистической физикой положение о равнораспределении энергии по степеням свободы молекул. Если предположить, что ни один из видов движения не имеет преимущества перед другими, то на любую степень свободы поступательного, вращательного и колебательного движений должна приходиться в среднем одинаковая энергия, равная
поскольку ни одно из направлений поступательного движения не имеет преимущества. Однако в природе наряду с поступательным движением возможны вращение молекул и колебания атомов в молекуле, входящих в состав молекул. Эти виды движений, также как и поступательное движение, связаны с некоторым запасом энергии, определить который позволяет устанавливаемое статистической физикой положение о равнораспределении энергии по степеням свободы молекул. Если предположить, что ни один из видов движения не имеет преимущества перед другими, то на любую степень свободы поступательного, вращательного и колебательного движений должна приходиться в среднем одинаковая энергия, равная 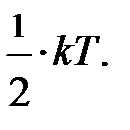 В этом и состоит суть положения о равнораспределении энергии по степеням свободы. Из этого предположения следует, чем сложнее молекула, тем больше число её степеней свободы, тем больше среднее значение энергии одной молекулы
В этом и состоит суть положения о равнораспределении энергии по степеням свободы. Из этого предположения следует, чем сложнее молекула, тем больше число её степеней свободы, тем больше среднее значение энергии одной молекулы  ; здесь
; здесь 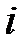 – сумма поступательных, вращательных и колебательных степеней свободы
– сумма поступательных, вращательных и колебательных степеней свободы  . Из школьного курса известно, молекула кислорода, азота состоит из двух атомов, соответственно,
. Из школьного курса известно, молекула кислорода, азота состоит из двух атомов, соответственно, 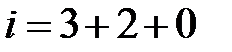 .
.

 не так-то просто проверить на опыте. Да, мы умеем измерять на опыте давление газа, но у нас нет приборов для прямого измерения величины энергии Е = Е 1× n. Человечество вообще не умеет измерять внутреннюю энергию газа в состоянии теплового равновесия. Чтобы реально использовать уравнение кинетической теории газов, приходится прибегать к процедуре косвенных измерений величины Е (энергии). Для этого человечество ввело величину, характеризующую состояние теплового равновесия для любых объектов. Читатель правильно догадался, такой величиной является температура; символ – Т.
не так-то просто проверить на опыте. Да, мы умеем измерять на опыте давление газа, но у нас нет приборов для прямого измерения величины энергии Е = Е 1× n. Человечество вообще не умеет измерять внутреннюю энергию газа в состоянии теплового равновесия. Чтобы реально использовать уравнение кинетической теории газов, приходится прибегать к процедуре косвенных измерений величины Е (энергии). Для этого человечество ввело величину, характеризующую состояние теплового равновесия для любых объектов. Читатель правильно догадался, такой величиной является температура; символ – Т.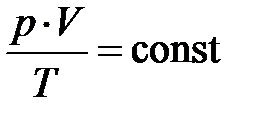 , если сорность и масса газа не изменяются. Эту формулу русский учёный Д.И. Менделееву в 1875 году обобщил для любой массы газа в виде
, если сорность и масса газа не изменяются. Эту формулу русский учёный Д.И. Менделееву в 1875 году обобщил для любой массы газа в виде  , –– объединённый газовый закон. Отсюда следует, при постоянном объёме и массы газа давление пропорционально температуре. Естественно ожидать, температура системы должна быть пропорциональна энергии частицы. Чтобы найти коэффициент пропорциональности между абсолютной температурой Т и энергией частицы Е 1, сопоставим обобщённое уравнение идеального газа и основное уравнение кинетической теории:
, –– объединённый газовый закон. Отсюда следует, при постоянном объёме и массы газа давление пропорционально температуре. Естественно ожидать, температура системы должна быть пропорциональна энергии частицы. Чтобы найти коэффициент пропорциональности между абсолютной температурой Т и энергией частицы Е 1, сопоставим обобщённое уравнение идеального газа и основное уравнение кинетической теории:
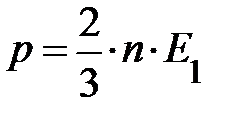 .
.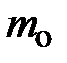 × N,
× N, 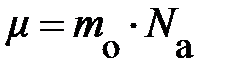 , а
, а  и, проявив терпение, проведёт преобразования первого уравнения, то испытает чувство глубокого удовлетворения, поскольку в результате его действий первое уравнение примет вид
и, проявив терпение, проведёт преобразования первого уравнения, то испытает чувство глубокого удовлетворения, поскольку в результате его действий первое уравнение примет вид  . После преобразований левые части уравнений системы равны, должны быть равны и правые. Отсюда немедленно следует, энергия одной молекулы
. После преобразований левые части уравнений системы равны, должны быть равны и правые. Отсюда немедленно следует, энергия одной молекулы  оказывается зависящей лишь от температуры, но не зависит от массы молекулы; буква k, равная
оказывается зависящей лишь от температуры, но не зависит от массы молекулы; буква k, равная  =
=  , называется постоянной Больцмана. Здесь весьма важно обратить внимание на формулу
, называется постоянной Больцмана. Здесь весьма важно обратить внимание на формулу  . Если имеется смесь из нескольких сортов газов, результирующее давление может быть записано
. Если имеется смесь из нескольких сортов газов, результирующее давление может быть записано 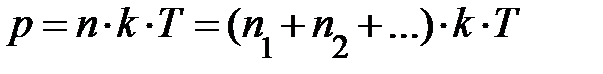 ; здесь
; здесь  – концентрация различных сортов газов. Выражение перепишем
– концентрация различных сортов газов. Выражение перепишем 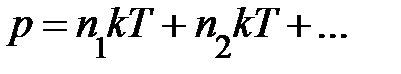 , отсюда немедленно следует закон Дальтона – давление смеси идеальных газов равно сумме парциальных давлений газов, образующих смесь.
, отсюда немедленно следует закон Дальтона – давление смеси идеальных газов равно сумме парциальных давлений газов, образующих смесь. поскольку ни одно из направлений поступательного движения не имеет преимущества. Однако в природе наряду с поступательным движением возможны вращение молекул и колебания атомов в молекуле, входящих в состав молекул. Эти виды движений, также как и поступательное движение, связаны с некоторым запасом энергии, определить который позволяет устанавливаемое статистической физикой положение о равнораспределении энергии по степеням свободы молекул. Если предположить, что ни один из видов движения не имеет преимущества перед другими, то на любую степень свободы поступательного, вращательного и колебательного движений должна приходиться в среднем одинаковая энергия, равная
поскольку ни одно из направлений поступательного движения не имеет преимущества. Однако в природе наряду с поступательным движением возможны вращение молекул и колебания атомов в молекуле, входящих в состав молекул. Эти виды движений, также как и поступательное движение, связаны с некоторым запасом энергии, определить который позволяет устанавливаемое статистической физикой положение о равнораспределении энергии по степеням свободы молекул. Если предположить, что ни один из видов движения не имеет преимущества перед другими, то на любую степень свободы поступательного, вращательного и колебательного движений должна приходиться в среднем одинаковая энергия, равная 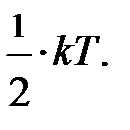 В этом и состоит суть положения о равнораспределении энергии по степеням свободы. Из этого предположения следует, чем сложнее молекула, тем больше число её степеней свободы, тем больше среднее значение энергии одной молекулы
В этом и состоит суть положения о равнораспределении энергии по степеням свободы. Из этого предположения следует, чем сложнее молекула, тем больше число её степеней свободы, тем больше среднее значение энергии одной молекулы  ; здесь
; здесь 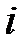 – сумма поступательных, вращательных и колебательных степеней свободы
– сумма поступательных, вращательных и колебательных степеней свободы  . Из школьного курса известно, молекула кислорода, азота состоит из двух атомов, соответственно,
. Из школьного курса известно, молекула кислорода, азота состоит из двух атомов, соответственно, 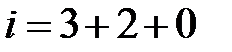 .
.


